Simulate from Kernel Density Estimate (empirical PDF)

Question

I have a vector X of N=900 observations that are best modeled by a global bandwidth Kernel density estimator (parametric models, including dynamic mixture models, turned out not to be good fits):

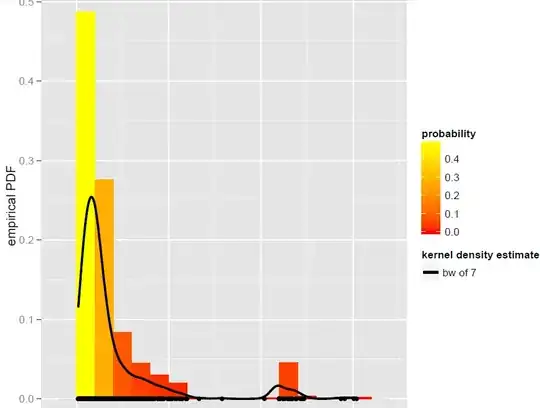
Now, I want to simulate from this KDE. I know this can be achieved by bootstrapping.

In R, it all comes down to this simple line of code (which is almost pseudo-code): x.sim = mean(X) + { sample(X, replace = TRUE) - mean(X) + bw * rnorm(N) } / sqrt{ 1 + bw^2 * varkern/var(X) } where the smoothed bootstrap with variance correction is implemented and varkern is the variance of the Kernel function selected (e.g., 1 for a Gaussian Kernel).

What we get with 500 repetitions is the following:

It works, but I have a hard time understanding how shuffling observations (with some added noise) is the same thing as simulating from a probability distribution? (the distribution being here the KDE), like with standard Monte Carlo. Additionally, is bootstrapping the only way to simulate from a KDE?

EDIT: please see my answer below for more information about the smoothed bootstrap with variance correction.

Answer 1

Here's an algorithm to sample from an arbitrary mixture $f(x) = \frac1N \sum_{i=1}^N f_i(x)$:

• Pick a mixture component $i$ uniformly at random.
• Sample from $f_i$.

It should be clear that this produces an exact sample.

A Gaussian kernel density estimate is a mixture $\frac1N \sum_{i=1}^N \mathcal{N}(x; x_i, h^2)$. So you can take a sample of size $N$ by picking a bunch of $x_i$s and adding normal noise with zero mean and variance $h^2$ to it.

Your code snippet is selecting a bunch of $x_i$s, but then it's doing something slightly different:

• changing $x_i$ to $ \hat\mu + \frac{x_i - \hat\mu}{\sqrt{1 + h^2 / \hat\sigma^2}} $
• adding zero-mean normal noise with variance $\frac{h^2}{1 + h^2/\hat\sigma^2} = \frac{1}{\frac{1}{h^2} + \frac{1}{\hat\sigma^2}}$, the harmonic mean of $h^2$ and $\sigma^2$.

We can see that the expected value of a sample according to this procedure is $$ \frac1N \sum_{i=1}^N \frac{x_i}{\sqrt{1 + h^2/\hat\sigma^2}} + \hat\mu - \frac{1}{\sqrt{1 + h^2 /\hat\sigma^2}} \hat\mu = \hat\mu $$ since $\hat\mu = \frac1N \sum_{i=1}^N x_i$.

I don't think the sampling disribution is the same, though.

Answer 2

To eliminate any confusion about whether it is possible or not to draw values from the KDE using a bootstrap approach, it is possible. The bootstrap is not limited to estimating variability intervals.

Below is a smoothed bootstrap with variance correction algorithm that generates synthetic values $Y_{i}'s$ from a KDE $K$ of window $h$. It comes from this book by Silverman, see page 25 of this document, section 6.4.1 "Simulating from density estimates". As noted in the book, this algorithm allows to find independent realizations from a KDE $\hat{y}$, without requiring to know $\hat{y}$ explicitly:

To generate a synthetic value $Y$ (from a training set $\big\{X_{1},...X_{n}\big\}$):

• Step 1: Choose $i$ uniformly with replacement from $\big\{1,...,n\big\}$,
• Step 2: Sample $\epsilon$ from $K$ (i.e., from the Normal distribution if $K$ is Gaussian),
• Step 3: Set $Y=\bar{X}+(X_{i}-\bar{X}+h.\epsilon)/\sqrt{1+h^{2}{\sigma_{K}}^2/{\sigma_{X}}^2}$.

Where $\bar{X}$ and ${\sigma_{X}}^2$ are the sample mean and variance, and ${\sigma_{K}}^2$ is the variance of $K$ (i.e., 1 for a Gaussian $K$). As explained by Dougal, the expected value of the realizations is $\bar{X}$. Thanks to the variance correction, the variance is ${\sigma_{X}}^2$ (on the other hand, the smoothed bootstrap without variance correction, where step 3 is simply $Y=X_{i}+h.\epsilon$, inflates the variance).

The R code snippet in my question above is strictly following this algorithm.

The advantages of the smoothed bootstrap over the bootstrap are:

• "spurious features" in the data are not reproduced as different values from the ones in the sample can be generated,
• values beyond the max/min of the observations can be generated.