5

Is there any way to test whether a series should be logged or transformed in another way?

I have a code of which i use to run lots of different data through to forecast. Some of the data definitely need transforming however some don't. As the code has been written to be fully automatic it will be used by non-statisticians within the company so they will have no idea whether they should change the code to transform the data depending on the series. So i need tests which will check that for them and apply the transformation accordingly.

Here is a example data set that you can use:

M <- matrix(c("08Q1", "08Q2", "08Q3", "08Q4", "09Q1", "09Q2", "09Q3", "09Q4", "10Q1", "10Q2", "10Q3", "10Q4", "11Q1", "11Q2", "11Q3", "11Q4", "12Q1", "12Q2", "12Q3", "12Q4", "13Q1", "13Q2", "13Q3", "13Q4", "14Q1", "14Q2", "14Q3",  5403.676,  6773.505,  7231.117,  7835.552,  5236.710, 5526.619,  6555.782, 11464.727,  7210.069,  7501.610,  8670.903, 10872.935,  8209.023,  8153.393, 10196.448, 13244.502,  8356.733, 10188.442, 10601.322, 12617.821, 11786.526, 10044.987, 11006.005, 15101.946, 10992.273, 11421.189, 10731.312),ncol=2,byrow=FALSE)
Nu <- M[, length(M[1,])]

I have found boxcoxfit() from the package geoR finds the lambda for transformation....does anyone know how accurate this is for transforming the data?

ml <- boxcoxfit(Nu)
  Fitted parameters:
    lambda    beta  sigmasq
      0.59  375.43  3649.39
N<- ((Nu^(ml$lambda))-1)/ml$lambda
Summer-Jade Gleek'away
  • 382
  • Perhaps heretical here, but an eyeball glance at your data suggests approximately linear trend, variability around it approximately constant, and obvious seasonality with peaks consistently in quarter 3. It's not obvious to me that any transformation helps at all. The fact that this is a rather short time series underlines that caution. This is all quite orthogonal to your request to automate analysis, naturally. – Nick Cox Oct 29 '14 at 20:01
  • @NickCox thankyou for your comment, i have many different types of data sets, some which give similar results to this and some that don't. e.g transactional and non-transactional data, i have found by analysing them that some definitly need transforming, however we are in the process of linking my code to a database in which data will automatically change and many data sets will be run. I need to find a way that decides if it should be transformed and how without me even looking at the data itself. – Summer-Jade Gleek'away Oct 30 '14 at 09:30
  • Indeed. But this thread implies that the task is highly challenging as even for a simple data series (a) different software yields different suggestions (b) different analysts don't agree. – Nick Cox Oct 30 '14 at 09:40
  • Yes i can see that... how inaccurate would the results be if i logged/transformed all the data sets straight away or just left them as they were? – Summer-Jade Gleek'away Oct 30 '14 at 09:49
  • It really does depends on the data and the decision. Any way, what does "inaccuracy" mean here? The key point is that the marginal distribution of a response variable may have little or nothing to do an appropriate time series model. @IrishStat's AUTOBOX is an attempt to build decisions into the program, so in effect the program designer is making your decisions for you. Looking at threads on this forum show that people disagree about strategy and style for time series just like anything else. – Nick Cox Oct 30 '14 at 10:20
  • The idea of selecting a transform based upon the untreated observations i.e. no model is illogical as the Gaussian assumptions are all about the error process NOT the observed time series . If the best ARIMA model is simply a mean model with no deterministic structure (pulses et al )then determining the transformation first would be appropriate ...Other than that the approach of transforming first is illogical and unwarranted and incorrect even though it may be easy to systematize..but that's just my opinion and anybody else who understands stuff. – IrishStat Oct 30 '14 at 10:41
  • @IrishStat ok so i have probably got this wrong so correct me if i have... basically i have to find the fitted values from an ARIMA/Holt-winters model and then i can proceed to see if the data should have been transformed and which transformation i should use, then run the model again on the transformed data? – Summer-Jade Gleek'away Oct 30 '14 at 10:46
  • I would generally agree with that strategy if and only if you have validated that there are no pulses, level shifts , local time trends in your residuals . For a more in-depth discussion of the error in taking logs of the airline series and the consequences of not treating anomalous data , please see http://www.autobox.com/pdfs/vegas_ibf_09a.pdf – IrishStat Oct 30 '14 at 11:06
  • thankyou for this link. I have sent it to my manager and he thinks that it would be worth learning to use this – Summer-Jade Gleek'away Oct 30 '14 at 11:58

2 Answers2

6

As @Irishstat points out you could use boxcox power transformation, which is a more general transformation function which also includes log transformation. R's forecast package has a function called BoxCox.lambda and BoxCox, you could use these two functions and determine if your data needs transformation. if lambda is close to 1 then your data needs no transformation, else you data needs appropriate power transformation.

Using your data 

x <- ts(c(5403.676,  6773.505,  7231.117,  7835.552,  5236.710, 5526.619,  6555.782, 11464.727,  7210.069,  7501.610,  8670.903, 10872.935,  8209.023,  8153.393, 10196.448, 13244.502,  8356.733, 10188.442, 10601.322, 12617.821, 11786.526, 10044.987, 11006.005, 15101.946, 10992.273, 11421.189, 10731.312),frequency =4)

lambda <- BoxCox.lambda(x, method=c("guerrero"))
lambda
0.3855427

x.transform <- BoxCox(x,lambda)
plot(x.transform)

Using the box.cox lambda yielded a lambda value 0.3855. You could use this in the BoxCox function as shown above.

Let us know if you find this post useful.

forecaster
  • 8,145
  • Have you any comment on why this recommendation (0.386) is quite different from 0.59? – Nick Cox Oct 29 '14 at 19:58
  • Box-Cox optimization requires a model. I guess if no model is specified then a simple mean model is used. Seems kind of silly to be talking about Box-Cox when no reasonable model is in place but that's just my opinion. Furthermore untreated outliers distort the Box-Cox optimization as it assumes no deterministic structure is present. – IrishStat Oct 29 '14 at 20:28
  • Power transformations ..other than -1,-.5 ,0.0,.5 ,1.0 are nigh impossible to justify when presenting a possible solution to a client . In my opinion it is an overkill to use values like .386 or .59 ....but that's just my opinion. – IrishStat Oct 29 '14 at 21:06
  • It doesnt have to be Box-Cox, thats just something i read about. – Summer-Jade Gleek'away Oct 30 '14 at 09:24
  • Thankyou forecaster. Just to clarify, when you say that if its close to 1 then it doesnt need a transformation...how close to 1 do you think it should be? 0.8? – Summer-Jade Gleek'away Oct 30 '14 at 09:25
  • @IrishStat If i use box-cox to find the lambda value, as you said it wouldnt be right to use values like 0.386 etc, would it be right to then round them to the nearest 0, .5, 1? or would this yeild innaccurate results? – Summer-Jade Gleek'away Oct 30 '14 at 09:52
  • If you are hell-bent to overly complicate your model and mis-analyze it using an unwarranted transformation then I would accept the rounding of the lambda. Notice in http://stats.stackexchange.com/questions/121553/confusing-holt-winters-parameters your forecasts are just too aggressive IMHO with respect to trend possibly due to the untreated anomaly at period 21 OR the assumed model that you have in place. – IrishStat Oct 30 '14 at 10:22
  • @IrishStat i have eight different models to forecast : ARIMA, ARIMA(putting weight on recent errors), Multiplicative HW, Additive HW, Multiplicative HW(weights on recent errors), Additive HW(weights on recent errors), Additive HW(optimizing parameters), Multiplicative HW(optimizing parameters) and i am creating a code which compares them against eachother looking at MAPE and other accuracy tests. So it will pick the best model. So would it just be better if i didnt transform any of my data? – Summer-Jade Gleek'away Oct 30 '14 at 10:36
  • Given the example that you provided there is no evidence of the need for a power transformation such as that delivered by Box-Cox . I believe this is what Nick Cox stated. Your approach to providing a list of models to try is somewhat similar to what I programmed in 1968 ... a list-based solution. The data should be able to formulate the model whilst you are shoe-horning the data into a pre-fixed set of trial models much like picking the best of 8 dresses off the rack rather than having the dress customized to your body. – IrishStat Oct 30 '14 at 10:45
  • @IrishStat But thats the thing, this data set may not need transforming but another one might and because its going to be a huge database with data running through my code from all over the world from my company then i cant personally analyse each set of data – Summer-Jade Gleek'away Oct 30 '14 at 10:48
  • Which is precisely why you shouldn't transformm first but rather simultaneously determine the best model and the best transform ala what I presented to you. Power transforms are like drugs ... some are good for you and some are not. They can have very negative side-effects on forecasts as has been pointed out time and time again by Chatfield and many others. Plase see http://stats.stackexchange.com/questions/6498/seeking-certain-type-of-arima-explanation/9017#9017 for a discussion of the Airline Series. – IrishStat Oct 30 '14 at 10:57
  • Ok that i understand...however i need to reproduce this using Rstudio...and I dont understand how to do this from the answer and example you gave, eg what is B, X1, A etc – Summer-Jade Gleek'away Oct 30 '14 at 11:06
  • B is the backshift operator (http://en.wikipedia.org/wiki/Lag_operator) , X1 is the empirically developed predictor series (0,0,0,0,0...,1,0,0,0,0 where the "1" is at period 21 and A is the error process resulting from estimation. – IrishStat Oct 30 '14 at 11:17
2

Power Transformations found via a Box-Cox test http://onlinestatbook.com/2/transformations/box-cox.html are useful/correct when a linear relationship is found between the expected value and the variability of the model errors. It has little to do with the variability of the original series. The range of transformations is from none to a reciprocal. Care should be taken to account for pulse outliers as untreated they can distort the Box-Cox conclusions. Furthermore note that error variance may also change in discrete steps quite free of the expected value . The appropriate remedy in this case is to Generalized Least Squares or as it is often known as Weighted Least Squares.

You might look very closely at my response to Seeking certain type of ARIMA explanation

UPON RECEIPT OF DATA (enter image description here :some 27 quarterly observations starting at 2008 q1

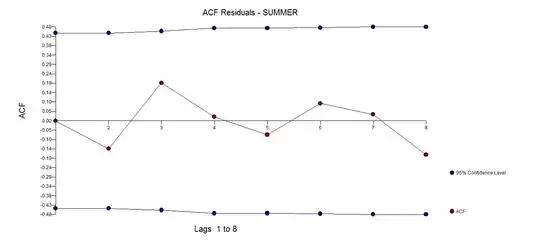The ACF of the original series suggests a fairly strong seasonal structure. AUTOBOX automatically identified a model enter image description here and shown here enter image description here which yielded an ACF of the error process suggesting model sufficiency enter image description here . The model includes an identified intervention at period 21 (2013 quarter 1 ) of the 27 observations. A plot of the actual and the cleansed highlights the anomaly.enter image description here The actual/fit/forecast graph is here enter image description here with forecasts here 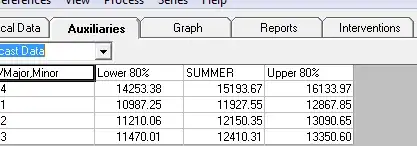enter image description here. In summary there was no need for any variance stabilization transformation for this data set. The optimal box-cox coefficient requires a model and in this case is 1.0. If you don't specify a model as is possible with boxcoxfit then in the absence of a good ARIMA structure and the identified anomaly at period 21 you might then get a lambda like .52 which is probably the result of an incorrect model.

Community
  • 1
IrishStat
  • 29,661
  • so is this suitable to apply to any series even if it may not need transforming? – Summer-Jade Gleek'away Oct 27 '14 at 15:07
  • Yes because if the error process is free of any of the structure I referenced then the conclusion will be No Transform is required. – IrishStat Oct 27 '14 at 15:09
  • ok great, so i can apply that to my code so everything automates :) thankyou :) – Summer-Jade Gleek'away Oct 27 '14 at 15:12
  • Just be careful that the error term from your model is free of ARIMA structure , Free of any Pulses/level-Step shifts , Local Time Trends and Pulses AND that you have verified t hat the model parameters are invariant over time OTHERWISE you may be pinning the tail on the wrong donkey . – IrishStat Oct 27 '14 at 15:18
  • ....How do i do all that? :/ – Summer-Jade Gleek'away Oct 27 '14 at 15:19
  • Since you asked , I have helped develop a solution that speaks to all of the things/items that I suggested. The software package AUTOBOX can be downloaded from AFS http://www.autobox.com/cms/ . There is a 30 day free trial version available , contact them to get more details. – IrishStat Oct 27 '14 at 20:25
  • If you wish to post your data I will try and demonstrate/show you what I mean in practice. – IrishStat Oct 28 '14 at 13:04
  • The data in the question is a data set that can be used as an explanation :) – Summer-Jade Gleek'away Oct 28 '14 at 13:06
  • Would you like my full code? – Summer-Jade Gleek'away Oct 28 '14 at 13:06
  • @Summer-JadeGleek'away IrishStat is outlining that his software offers a solution to your problem. If you want to do something exactly equivalent in R, it's likely to be a major programming project to match what AUTOBOX does. – Nick Cox Oct 29 '14 at 16:12