1

Can I write $\Phi(ax)$ as $b\Phi(x)$ for some constant $b$, please? FYI, $\Phi(\cdot)$ is the cdf for standard normal random variable. Is there such relationship?

Waldir Leoncio
  • 2,637
LaTeXFan
  • 1,306
  • 2
    Note that the first one will always be between 0 and 1 and the second one will always be between 0 and b. – power Jun 05 '14 at 07:30

1 Answers1

4

Your question doesn't specify but I assume you mean for some given constant $a$ and that the relationship should hold for all $x$ - i.e. that we should have a single $b$ that works for any $x$. (If you want $b$ to be a function of $x$, that's quite a different question)

This is quite clearly impossible, since $\Phi(ax)$ is bounded between 0 and 1. Since any value of $b$ other than $1$ will either make $b\Phi(x)>1$ for some $x$, or will make it unable to attain all values (because it will have a maximum smaller than the maximum value of $\Phi(ax)$).

Hence $b$ can only be $1$.

This then implies that $a$ can only be $1$.

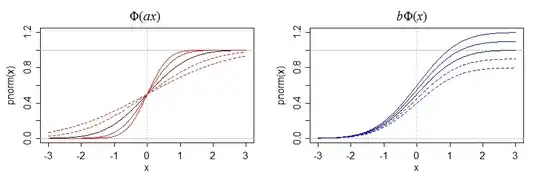
enter image description here

That is, the only way for this to be true across all $x$ is for both $a$ and $b$ to be 1.

Glen_b
  • 282,281
  • Sorry, I certainly mis-represented my question here. I am still working on this question http://stats.stackexchange.com/questions/101258/find-the-umvue-for-phi-mu – LaTeXFan Jun 05 '14 at 09:26
  • And I am trying to re-arrange the given integral so that I can find an unbiased estimator for $\Phi(\mu)$. Any ideas? – LaTeXFan Jun 05 '14 at 09:28