Compute $(e^x-1)/x$ near $x = 0$

Question

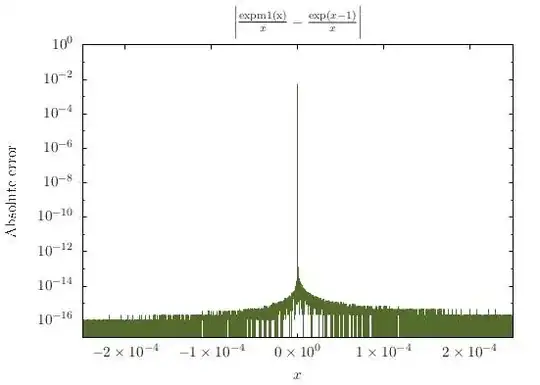
The function $f \colon x \mapsto (e^x-1)/x$ has singularity near $x = 0$. That singularity can be lifted, though: for $x = 1$, one should have $f(x) = 1$, since $$ e^x = \sum_{k=0} \frac{x^k}{k!} $$ and thus $$ (e^x - 1)/x = \sum_{k=1} \frac{x^{k-1}}{k!} $$ However, the form $(e^x-1)/x$ is not only not defined at $x = 0$, it is also numerically unstable in the vicinity of that point; in order to evaluate $f(x)$ for very small $x$ numerically, one could use a Taylor expansion, i.e. a truncation of the afore-mentioned power series.

Q: Does the function $f$ have a name? In other words, is this a common problem?

Q: Is anyone aware of a C/C++ library that handles this situation nicely, i.e. uses the Taylor expansion of an appropriate degree near 0 and the other representation away from zero?

n00b · Accepted Answer · 2013-09-01T12:50:41.403

19

Possibly one could start with the function $\mathtt{expm1}$ which is part of the C99 standard, and calculates $e^x-1$ accurately near $x=0$.

edited Sep 01 '13 at 12:50

answered Aug 30 '13 at 20:14

n00b

590
3
11

Juan M. Bello-Rivas · Answer 2 · 2013-09-07T22:52:11.387

17

This is an instance of cancellation error. The C standard library (as of C99) includes a function called expm1 that avoids this problem. If you use expm1(x) / x instead of (exp(x) - 1.0) / x, you won't experience this issue (see graph below). <code>fabs(expm1(x) / x - (exp(x) - 1.0) / x)</code>

The details and solution of this particular problem are discussed at length in Section 1.14.1 of Accuracy and Stability of Numerical Algorithms. The same solution is also explained in page 19 of W. Kahan's paper titled How Futile are Mindless Assessments of Roundoff in Floating-Point Computation?. The actual implementation of expm1 in the GNU C library is different from the approach described in the references above and is thoroughly documented in the source code.

edited Sep 07 '13 at 22:52

answered Aug 30 '13 at 20:14

Juan M. Bello-Rivas

3,994
16
24

1

Thank you, that's just what I needed! Unfortunately, I can only accept one answer... – anonymous Aug 31 '13 at 00:02
Of course! No problem :-) – Juan M. Bello-Rivas Aug 31 '13 at 00:04

score 3 · Answer 3 · answered Aug 30 '13 at 21:06

To answer your first question, no, the function doesn't have a name (at least not one that is widely known).

As others have mentioned, the best way to compute the function is to treat several special cases. This is how any library would compute the function.

Case 0: x = 0, return 1.
Case 1: $|x|<\delta$, return $1+x/2$. Choose $\delta$ empirically for your numerical precision and data type. For double, it should be about 2e-8. For float, it's about 5e-4.
Case else: return expm1(x)/x.

You can be more sophisticated and special case more things with truncated Taylor series, but it's probably not worth it. In fact, it's not entirely clear that case 1 needs to be handled separately, since as k20 pointed out, the cancellation is safe. However, handling it separately would let me feel more confident about it.

score 2 · Answer 4 · edited Apr 13 '17 at 12:19

2

I remember this question having been asked earlier on this site, and surprisingly the answer is that you only need to special-case exact equality to zero. The errors cancel out near zero. I don't have the link.

Yeah this answer was completely wrong. I'm not sure why it was upvoted so much, probably because it was stated so authoritatively. I found the link I had in mind. It was on the math stackexchange here, not on the scicomp stackexchange. The expm1-free error cancellation formula is given in the answer by J.M. and uses a u = exp(x) transformation.

edited Apr 13 '17 at 12:19

Community

1

answered Aug 30 '13 at 19:14

k20

772
3
3

Right. If $x$ = infinitessimal $dx$, $(e^{dx} - 1)/dx$ = $(1+dx - 1)/dx$ = $1$.

Mike Dunlavey

Aug 30 '13 at 21:00

1

I don't think this works for $dx$ small enough since then in floating point accuracy, $1+dx=1$ and the whole thing blows up. – Wolfgang Bangerth Aug 30 '13 at 21:48

score 0 · Answer 5 · answered Feb 12 '17 at 16:18

0

To answer the first question and provide a (probably numerically inefficient) method for the second, note that this is the inverse of the generating function of the Bernoulli numbers.

answered Feb 12 '17 at 16:18

Nikolaj-K

176
3

That's an interesting connection, thanks for pointing that out. Unfortunately, I believe the triple sum will render this prohibitively expensive. Moreover, it is not immediately clear where to truncate each sum to obtain the desired accuracy. – anonymous Feb 17 '17 at 12:43
@anonymous: Which tripple sum do you mean? You don't need the Bernoulli polynomials, only the Bernoulli numbers, and you can list those in advance. But yes, it's still not to be better than the Taylor series. – Nikolaj-K Feb 19 '17 at 02:46
You can compute those in advance if it's clear that you only need a fixed finite number for any input only, though. – anonymous Feb 19 '17 at 10:25
@anonymous: Well yes, just like you'd list the Taylor coefficients in advance. – Nikolaj-K Feb 24 '17 at 21:02

Compute $(e^x-1)/x$ near $x = 0$

5 Answers5

Linked