5

The real-life problem

Assume I put a spherical roast with initially constant temperature of start_temp=25 (°C) into an oven with oven_temp=80. A meat thermometer is inserted at the core.

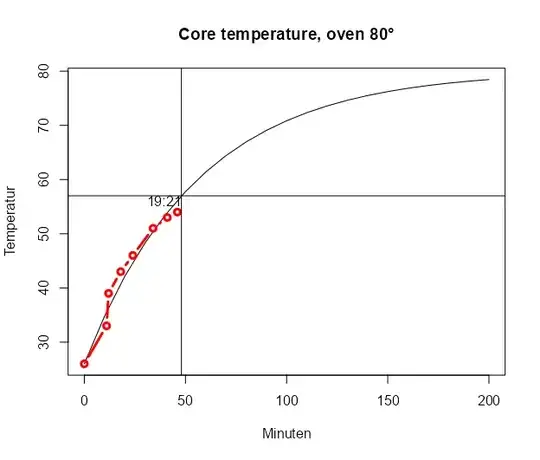
At what time will the roast be ready, i.e. at target_temp=57?

No discussion about rare or well-done, please, this is serious science. The assumption of a constant initial temperature in the sphere is a bit frivolous because the roast is usually fried in a pan before inserting it into the oven, but let's keep this for further research.

The theory

As of the Fourier expansion of heat transfer, page 43, this can be approximated by an exponential curve.

tfun = function(time,  th) {
  start_temp + (oven_temp - start_temp) * (1 - exp(-time / th))
}

Using more terms of the Fourier series expansion is easily possible, but does not contribute to the fit quality.

Measured and fitted core temperature with prediction of time roast is ready

We do not care that estimates of thermal conductivity and radius could give us an initial approximation, because the fit works reasonably and gives a good estimate of the time when the family has to stop playing Flight Simulator. See the R-program below.

The extended real-life problem

The family suddenly request that the temperature should be lowered to 60 degrees for a more even meat texture or more time to finish the landing. So at t= 30 minutes, we switch the oven from 80° to 60°; assume it cools immediately.

The extended theory

This requires me to solve the inhomogeneous equation with a step function at the boundary, with all the nasty singularities at the center (Thibault et al.). I failed to get it to work with simulated data.

Does anyone have an idea for a simplified fit piecewise function to use? The final code will be in c# (on Android), but Python or R are fine.

The wild extension:

There are Bluetooth-devices with two sensors, so one could be inside the meat, the other in the oven. This would mean that oven temperature and roast core temperature are given in a minute-grid.

# At what time can we serve the roast?

https://pnp.mathematik.uni-stuttgart.de/igt/eiserm/lehre/HM3/HM3-S-1x2.pdf


page 43


d = data.frame(
  time = c("18:33", "18:44", "18:45", "18:51", "18:57", "19:07", "19:14", "19:19"),
  temp = c(26, 33, 39, 43, 46, 51, 53,54 )
)
d$tmin = as.numeric((strptime(d$time, "%H:%M") - strptime(d$time[1], "%H:%M")) /
                      60)
oven_temp = 80 # Oven temperature, constant
target_temp = 57 # Requested core temperature


start_temp = d$temp[1]
tfun = function(time,  th) {
  start_temp + (oven_temp - start_temp) * (1 - exp(-time / th))
}


I am using a nonlinear fit here. Fitting linear regression


to log-data works fine, but would not be generalizable


to more complex functions.


coef(nls(temp ~ tfun(tmin, th), start = list(th = 50), data = d))


time = seq(0, 200, by = 10)
th_1 = coef(nls(temp ~ tfun(tmin, th), start = list(th = 90), data = d))


plot(
  time,
  tfun(time, th_1),
  type = "l",
  ylab = "Temperatur",
  xlab = "Minuten",
  main = paste0("Core temperature, oven ", oven_temp, "°")
)
lines(d$tmin, d$temp,col = "red",lwd = 3, type = "b")
abline(h = target_temp)


tfun_target = function(time, th) {
  tfun(time, th) - target_temp
}


target_minute = as.integer(uniroot(tfun_target, c(0, 300), th = th_1)$root)
abline(v = target_minute)
text(target_minute,
     target_temp,
     adj = c(1, 1),
     format(strptime(d$time[1], "%H:%M") + target_minute * 60, "%H:%M"))
Dieter Menne
  • 161
  • 4
  • It seems to me that the outcome depends on such things as air versus meat conductivity, as the surface of the roast is now hotter than the air surrounding it, but also hotter than the adjacent meat (going inwards). I think we can formalize this as the transitory self-cooking regime, which ends when the roast boundary reaches ambient oven temperature. – Sardine May 24 '23 at 12:56
  • What you describe is "slow cooking", where the oven has the target temperature of the meat (e.g. 57 °), which requires 5 hours or more. It was very popular 20 years ago, but has fallen a bit out of favor in the oven, being replaced by "Sour vide" which is in a water bath. What I am referring to is the classical "resting phase", where the oven temperature is typically about 20 degrees above the target temperature, and 30 minutes to 2 hours in that situation. – Dieter Menne May 24 '23 at 17:47
  • I meant that if you reduce the oven temperature, and the meat boundary is at a temperature higher than the one you just set the oven to, then heat transfer will occur i) within the meat towards the center and ii) from the meat to the exterior. As such, it is the meat cooking itself, with the help of the oven merely decelerating the outwards heat transfer! – Sardine May 24 '23 at 22:14
  • It would be helpful to write here the equation that governs the heat transfer process; that would probably make the discussion more relevant and appealing. – Maxim Umansky May 24 '23 at 22:29
  • When you assume an infinitely long roastbeef with homogeneous meat, you can switch to cylindrical coordinates and write down the heat equation there, and by symmetry you'll obtain a one-dimensional equation in the radius-coordinate. This is easy to solve numerically, regardless of the initial conditions being a step function at the surface of the roast. – davidhigh May 28 '23 at 11:06
  • Regarding the previous comment: I overlooked that you want to use spherical coordinates (which drom the first I find not that suitable for a roastbeef). Anyways, the same approach works here as well -- you can solve a one-dimensional equation in the radial coordinate. – davidhigh May 28 '23 at 11:27
  • German roastbeefs are so small, that in effect they shrink to spheres when when pre-fried. Cylindrical or spherical coordinates are only different by a factor of 2 or 3 for the singular point at the center. See https://scicomp.stackexchange.com/questions/8609/implicit-heat-diffusion-with-kinetic-reactions – Dieter Menne May 28 '23 at 16:44

1 Answers1

1

Below is my wild guess at estimating the core temperature using a simplified version of the temperature at the center of a sphere. It "looks good", but the good look comes at the price of a value thermalDiffusivity much different from the literature.

Since I only care about the time the target temperature is reached, and data will be fitted to recorded temperatures, this is not that relevant - but it makes me think that there is something seriously wrong.

Looks like I cannot post images; see temperature graph. At 10 minutes, oven temperature is reduced from 80 to 60. Target temperature of 56 degrees is reached after 50 minutes.

using System.Windows.Forms.DataVisualization.Charting;

public class SphereTemperature
{
  public static void Main()
  {
    // Constants
    double initialTemperature = 25;  // Initial temperature of the sphere in °C
    double targetTemperature = 56;  // Target temperature to stop


// Sphere properties
double radius = 0.08;  // Radius of the sphere in meters
// Thermal diffusivity of water in m^2/s (Wikipedia)
//double thermalDiffusivity = 0.2e-6; // should be
double thermalDiffusivity = 0.5e-4; // "looks good", trial and error

// Time parameters
double deltaT = 10;  // Time step size in seconds

// Create a list to store the temperature
List<double> temperature = new() { initialTemperature};

double currentTime = 0;
double tNew = initialTemperature;

while (tNew < targetTemperature)
{
  temperature.Add(tNew);
  currentTime += deltaT;
  double ovenTemp = OvenTemperature(currentTime);
  // This line is a bit ....
  double grad = thermalDiffusivity * (ovenTemp - tNew) / radius;
  tNew += grad * deltaT;
}

// Plot the temperature over time
// DrawChart(temperature, deltaT);



}


private static double OvenTemperature(double currentTime)
  {
    // After 10 minutes, switch from 80 to 60
    return currentTime <= 600 ? 80 : 60;
  }
}
Dieter Menne
  • 161
  • 4