EDIT: Added another, more suitable, example below.
Disclaimer: With edge map I mean an image given as bitmap just consisting of black and white pixels.
Short description:
Briefly, I'm searching for fast, practical algorithms (or, even better, working implementations) to extract the parameters of (complete, possibly rotated) geometric objects from images give as bitmap as the following, in order to find objects which are "special" (e.g. in the sense of being completely included in another one like the small ellipse on the right). Is the Hough Transform or a successor the way to go?
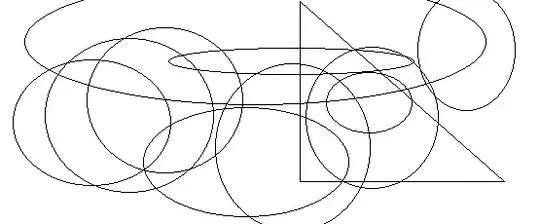
More details:
In particular, I'm searching for triangles, rectangulars, and ellipses of images where the edges are already (perfectly) extracted. As mostly (possibly rotated) ellipses occur, which seemingly are the hardest objects, I'd like to start with these. As the example illustrates, some objects only partially lie in the image and should be discarded (i.e. can be seen as kind of distortion or noise. This noise can be seen as ellipses with relatively huge axes). Overlapping objects, however, should be detected. I have rough bounds on the axes' parameters.
After having found the parameters I want to pick specific objects, for example the ones which are completely included in another one. Maybe detecting all objects in order to achieve this is too excessive?
My research so far:
Up to now, I stumbled accross several algorithms and implementations. Most notably based on the Hough Transform, which solves the problem in the (dual) parameter space using a voting scheme. However, the general Hough transform is rather slow. The implementations from 3, 4,5, and 6 should be faster but are not suited for the images at hand or I'm just too dumb to apply them correctly (which can absolutely be the case). At least for me, the implementations were either "confused" by the distorting, incomplete objects (whoch can be several hundreds), or did not find all objects. Since I only care about completed objects with intact edges, maybe some sort of edge following might also work?
My question:
As I'm not experienced in the image/object detection at all, I don't know whether I'm on the right track when considering the Hough transform for my problem. Is it the way to go, or do you know other algorithms or existing implementations solving the task at hand?
EDIT: As the ellipses are the main problem, which was not represented sufficiently good, I'll add another image. Again, this is just a part of the image which is provided as bitmap consisting of black and white pixels. I highlighted the ellipsis within the ellipsis in blue, while the other complete ellipsis is highlighted brown-ish. In general, there might be up to 30 objects of interest but few hundered disturbing ones (Isn't this always the case?! :/ ). Another, so far missing, information is that the "noisy", incomplete ellipses are different by having larger axes compared to the rather small wanted objects! (I'll also add the information above). Maybe the Hough transform becomes practical if I can find suitable parameter ranges for the small ellipses. Another idea just popping into my mind is that of detecting segments and deleting those with too low slope.
