2

I am trying to implement the Laplacian operator using Fourier Transform differentiation (https://en.wikibooks.org/wiki/Parallel_Spectral_Numerical_Methods/Finding_Derivatives_using_Fourier_Spectral_Methods#Taking_a_Derivative_in_Fourier_Space). I am comparing my Fourier differentiation with a periodic Laplacian in real space.

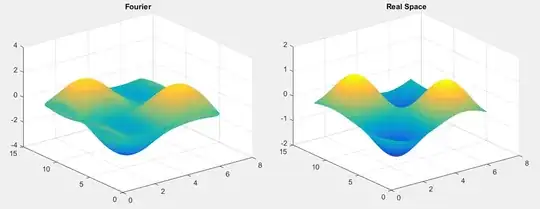
When my function is cos(x)*cos(y), the two results (real and Fourier space) agree with each other: enter image description here

But, when my function is sin(x)*sin(y), the Fourier space Laplacian has strange oscillations in it (the general shape remains the same). In the figure below, you can see that the left figure (the Fourier space differentiation) is a little fuzzy:

enter image description here

An example cross section through the above left figure looks like: enter image description here

I am very confused why these oscillations are appearing, and I would appreciate a solution. I suspect it may have something to do with aliasing, but I have been unable to pinpoint the issue or a solution.

Please find my code for implementing the Fourier space Laplacian here:

Nx = 512;
Ny = 256;

Lx = 2 * pi;
Ly = 4 * pi;

x = linspace(0, Lx, Nx)';
y = linspace(0, Ly, Ny)';

dx = x(2) - x(1);
dy = y(2) - y(1);

% Fourier space vectors
kx = 2*pi/Lx*[0:Nx/2-1 0 -Nx/2+1:-1]'; 
ky = 2*pi/Ly*[0:Ny/2-1 0 -Ny/2+1:-1]';

[x_grid, y_grid] = meshgrid(x, y);
[kx_grid, ky_grid] = meshgrid(kx, ky);

v = sin( 2*pi*x_grid ./ Lx ) .* sin( 2*pi*y_grid ./ Ly ); % Test Function
v_hat = fft2(v); % FFT of test function

% Fourier Space Laplacian
w_L = -( kx_grid.^2 + ky_grid.^2 ) .* v_hat;
w_L = real(ifft2(w_L));

% Periodic Real Space Laplacian
L = Laplacian_2D(v, dx, dy);

c = 10; % Because the edges get very weird
figure; mesh(x(c + 1:end-c),y(c + 1:end-c),w_L(c + 1:end-c,c+1:end-c)); title('Fourier');
figure; mesh(x(c + 1:end-c),y(c + 1:end-c),L(c + 1:end-c,c+1:end-c)); title('Real Space');

Also please find my 2D periodic Laplacian here:

function out = Laplacian_2D( f, hx, hy )

    f = f';
    [r c] = size(f);
    out = zeros(r, c);

    out( 2 : end - 1, 2 : end - 1 ) = ...
        ( f( 3 : end, 2 : end - 1 ) - ...
        2 * f( 2 : end - 1, 2 : end - 1 ) + ...
        f( 1 : end - 2, 2 : end - 1 ) ) / hx^2 + ...
        ( f( 2 : end - 1, 3 : end ) - ...
        2 * f( 2 : end - 1, 2 : end - 1 ) + ...
        f( 2 : end - 1, 1 : end - 2 ) ) / hy^2 ;

    % Remember (i, j)
    %  i = row, j = column
    %  i = y, j = x
    % but we transposed so we can say i = x, j = y

    % Periodic boundary conditions

    % 4 corners
    out( 1, 1 ) = ...
        ( f(2, 1) - 2 * f(1, 1) + f(end, 1) ) / hx^2 + ...
        ( f(1, 2) - 2 * f(1, 1) + f(1, end) ) / hy^2;
    out(1, end) = ...
        ( f(2, end) - 2 * f(1, end) + f(end, end) ) / hx^2 + ...
        ( f(1, 1) - 2 * f(1, end) + f(1, end - 1) )/ hy^2;
    out(end, 1) = ...
        ( f(1, 1) - 2 * f(end, 1) + f(end - 1, 1) ) / hx^2 + ...
        ( f(end, 2) - 2 * f(end, 1) + f(end, end) ) / hy^2;
    out(end, end) = ...
        ( f(1, end) - 2 * f(end, end) + f(end - 1, end) ) / hx^2 + ...
        ( f(end, 1) - 2 * f(end, end) + f(end, end - 1) ) / hy^2;

    % edges
    out( 1, 2 : end - 1 ) = ...
        ( f(2, 2 : end - 1) - 2 * f(1, 2 : end - 1) + f(end, 2 : end - 1) ) / hx^2 + ...
        ( f(1, 3 : end) - 2 * f(1, 2 : end - 1) + f(1, 1 : end - 2) ) / hy^2;
    out( end, 2 : end - 1 ) = ...
        ( f(1, 2 : end - 1) - 2 * f(end, 2 : end - 1) + f(end - 1, 2 : end - 1) ) / hx^2 + ...
        ( f(end, 3 : end) - 2 * f(end, 2 : end - 1) + f(end, 1 : end - 2) ) / hy^2;

    out( 2 : end - 1, 1) = ...
        ( f(3 : end, 1) - 2 * f(2 : end - 1, 1) + f(1 : end - 2, 1) ) / hx^2 + ...
        ( f(2 : end - 1, 2) - 2 * f(2 : end - 1, 1) + f(2 : end - 1, end) ) / hy^2;
    out( 2 : end - 1, end) = ...
        ( f(3 : end, end) - 2 * f(2 : end - 1, end) + f(1 : end - 2, end) ) / hx^2 + ...
        ( f(2 : end - 1, 1) - 2 * f(2 : end - 1, end) + f(2 : end - 1, end - 1) ) / hy^2;

    out = out';

end
Geoffrey Xiao
  • 105
  • 5
  • Not that this is the problem, but what's the range on the real space (fig 4)? It looks like the sign wave does not reach 0 on the boundaries. – Charles Mar 27 '17 at 01:41
  • I modified the plotting range to not display the boundaries because sometimes the boundaries blew up. This is in the last 3 lines of the first code segment (the variable c). Real space range is x = [0, 2*pi], y = [0, 4*pi]. – Geoffrey Xiao Mar 27 '17 at 02:01
  • 1
    Again, I'm not sure if this is the problem but I know that, when solving ODEs using periodic BCs, you must include only node points 1 through N-1, where N is the number of node points. That is, one of the two boundary points should be present in the computational domain. This is not an issue for cell centered data since all points are interior to the boundaries. – Charles Mar 27 '17 at 04:34
  • For the domain should it affect the differentiation? I was also playing around with the code and I saw that if I changed k to 2pi/Lx[0:Nx/2 -Nx/2+1:-1]' vs 2pi/Lx[0:Nx/2-1 0 -Nx/2+1:-1]', the interior no longer had fuzzy oscillations. But this change causes the endpoints to show the fuzzy oscillations instead. Any thoughts? – Geoffrey Xiao Mar 27 '17 at 15:35
  • How about using this instead: dx = Lx/Nx; dy = Ly/Ny; x = linspace(0, Lx-dx, Nx)'; y = linspace(0, Ly-dy, Ny)'; – Charles Mar 27 '17 at 21:38
  • My best explanation to see why this works (if it does) is that this is how the discrete equations turn out. I would suggest looking at the discrete form of the equations (pen & paper). – Charles Mar 27 '17 at 21:40

2 Answers2

5

1) You have misinterpreted the order the fft2 output elements are stored. This is a very common mistake, since it is very easy to get confused. Thankfully, there is an easy way to avoid such bugs. Arrange the Fourier space vectors the "natural way"

% Fourier space vectors kx = 2*pi/Lx*[-Nx/2:Nx/2-1]'; ky = 2*pi/Ly*[-Ny/2:Ny/2-1]';

Then, make sure the fft2 output has the same arrangement by using the ifft function. This hardly adds any computation load to your code.

v_hat = fftshift(fft2(v)); % FFT of test function

Perform the algebra in the Fourier space as before and then make the inverse shift to the input of ifft2, by using the ifftshift function.

w_L = real(ifft2(ifftshift(w_L)));

2) As you noticed, things get "very weird" at the edges. This is another issue, which has not to do with bugs or numerical accuracy, but with the convergence properties of the Fourier series transform. When the function to be transformed is continuous, the Fourier series has absolute convergence. But, when there are discontinuities, the Fourier series converges by norm, which means that only the measure of the difference between the truncated series and its limit goes to infinity, hence these "weird" oscillations at the edges, called "Gibbs oscillations".

However, it may not be clear what the source of the discontinuity is. After all, v and its derivatives are well behaved functions. This has to do with the discrepancies with the Fourier series transform (FST) and the discrete Fourier transform(DFT). FST acts on periodic functions, whereas DFT on discrete signals of finite length. In order to interpret DFT as a numerical approximation to FFT, we implicitly assume that the input of DFT represents a sample of some periodic signal, whose half-period is represented by this window and the other half by its mirror image. This is, of course, easier to visualize in the 1D case. Therefore, every function whose sample is not zero at the window edges is implicitly interpreted as discontinuous. v may be zero at the edges, but its Laplacian is not and this makes these spooky Gibbs oscillations appear as if from nowhere.

zap
  • 220
  • 1
  • 6
  • I tried to account for this by redefining my k vectors. Is my k vector incorrect perhaps? In MATLAB, say Nx=8 and data is size Nx. Will the resulting fft(data) indices be [1 2 3 4 -3 -2 -1 0] or [0 1 2 3 4 -3 -2 -1]? Also why do you define k as -Nx/2+1:Nx/2? Others define k as -Nx/2:Nx/2-1 http://scicomp.stackexchange.com/questions/5314/order-of-matlab-fft-frequencies. – Geoffrey Xiao Mar 29 '17 at 16:14
  • 2
    You re absolutely right, it should be -Nx/2:Nx/2-1. I will edit this in my answer above. The indices will be [0 1 2 3 -4 -3 -2 -1]. In the 2D it becomes more complicated. My advice is to try not to guess what the fft output order is. This is a source of mental friction and bugs that may be hard to find. Use the helper functions fftshift and ifftshift and you will never have to worry about it again. – zap Mar 29 '17 at 17:52
1

I just tried running this, and it seems to remove the oscillations, so I'll add this as an answer. I suggest you change your code as follows, before your linspace definition for coordinates, add and modify the lines to read:

 x = linspace(0, Lx, Nx+1)'; x = x(1:Nx);
 y = linspace(0, Ly, Ny+1)'; y = y(1:Ny);

I suggest you write out the discrete form of the equations to see why the last point should not be included (it is repeated if you do include it).

I've updated my answer, thanks to @Richard Zhang, because my original suggestion was susceptible to precision errors.

Charles
  • 619
  • 1
  • 5
  • 12