1

I am trying to exert a desired load of 0.07 N.m on a BLDC motor shaft whose length is 0.750in and diameter is 0.3125in (0.008m). I can go to a machine shop and get a small adjustable cylindrical coupling made for my shaft. But I need it to exert close to desired torque at a speed of 2100 rpm (220 rad/s). I tried doing some calculations, according to the formula

Torque = speed * mass * (radius)^2

If I solve this equation with T = 0.07 N.m, speed = 220 rad/sec, radius = 0.004 m, I get around 20 kg for mass, which is huge!!!. It is more than the mass of the motor. Can you please suggest a convenient way to load the motor. Thank you.

Adeel
  • 23
  • 1
  • 5
  • We could help you more if we knew what you were trying to do! – Mark Omo May 03 '15 at 14:51
  • I am actually trying to test speed regulation characteristics of the BLDC motor drive, under a PI type control. I have the motor and the driving circuit. But I do not have anything to load the motor with. So all I need is something that will act as a mechanical load on the shaft. I hope it clarifies. – Adeel May 03 '15 at 15:10

2 Answers2

1

There are a couple ways you could test this with a constant load:

  • do what you said by applying a load, you could use a spool 2cm in diameter with a string holding a 1kg mass down giving .09Nm of force (you could fine tune the mass or pulley diameter) this has the advantage of subtly changing components (mass of string/diameter of pulley) allowing you to more thoroughly test your PI controller, but the disadvantage of a limited time of function depending on the length of string and the desired rotation speed (the rotation rate has no effect on the torque unless it is changing and the pulley has a non neginlabal rotational inertia.

  • You could put vanes on the motor and put them them in a tub of water, which will produce torque but this will be dependent on the rotation speed of the vanes and will be hard to predict and will need to be measured and tested. However this has several advantages, practically unlimited run time and very constant torque at speeds slow enough that nothing weird happens to the water (excessive waves/cavitation ect...) but, this will require experimentation and a test stand setup.

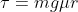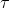  • Another option would be to spin a wheel with a brake pad attached with a known or measured coefficient of friction this will allow you to apply precise repeatable force on the wheel by easily adjusting the mass that of the object sitting on top of the wheel. You can calculate it using the following formula, formula where tau is the torque desired, 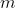m is the mass, 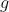g is the acceleration of gravity 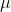mu is the measured or calculated coefficient of kinetic friction and r is the radius of thew wheel. This all assumes the friction force is directed straight down (e.g. resting on top of the wheel). This is probably the best solution as you can easily vary the friction force and ius is very repeatable and accurate, additionally allowing unlimited run time limited only by the wear of the materials (which could be non negligible depending on the speed and the materials used.

Community
  • 1
Mark Omo
  • 1,919
  • 13
  • 23
  • Thank you Mark. These are great ideas, especially the one with vanes immersed in water. – Adeel May 04 '15 at 18:41
0

You may find the wikipedia Dynamometer article useful. The “Types of Dynamometers” section lists eight kinds of dynamometers. (Mark Omo's answer corresponds to two or three of the several types.)

If you have several sizes of power resistors available, you could connect a DC generator (or a DC motor used as a generator) to a resistor and use that system as a load on the motor under test. Resistor substitutions or a high-wattage rheostat can make the load variable.

James Waldby - jwpat7
  • 1,991
  • 1
  • 11
  • 12
  • I actually have another BLDC with comparable ratings. I got mounting manufactured for the two BLDC's. Now if, instead of a DC generator, I want to use a three phase BLDC, I am guessing that I'll have to connect my load in star or delta configuration in order to load all three phases, correct? Also, if the three phase load is unbalanced, will the torque not be uniform? (It may be too many questions... sorry) – Adeel May 04 '15 at 18:44
  • An uncharacterized motor won't work out well as the load portion of a dynamometer system. But see an instructables thread, about BLDCs as generators. ¶ I think a cheap, brushed DC motor might do. For formula links, please see my answer to question #5209. ¶ Old exercise equipment is a cheap source of loading devices, eg eddy current absorbers, band or caliper brakes, etc. – James Waldby - jwpat7 May 04 '15 at 19:55