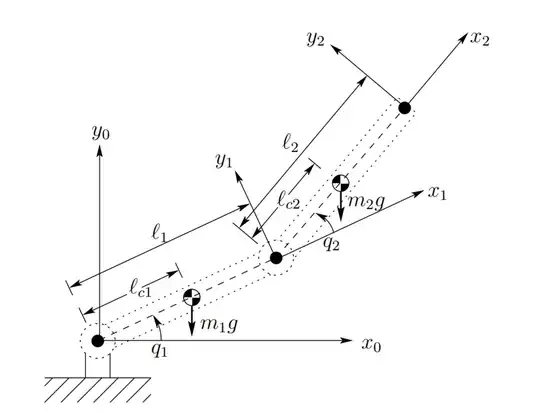
So we all know (and love) the typical dynamic equation of a robotic arm:
$$ M(q) \ddot{q}+C(q,\dot{q})\dot{q}+G(q)=\tau $$
Where M is the mass matrix, G is gravity and C is Coriolis and Centrifugal forces.
Coriolis and Centrifugal forces are pseudo forces that are experienced only for the frame that is attached to the body that is rotating. But my understanding is that all calculations happen relative to the base frame, which is static. The need for Coriolis and Centrifugal forces would imply that the forces are actually expressed in the frame that is attached to each link.
To put my question simply, why do we need the coriolis and centrifugal forces in the dynamic equation of a robotic arm (since everything is done relative to the initial/base frame)?
(p.s. feel free to use a single or double pendulum robotic arm example if you would prefer).