The general formula, as given by OP, is actually the most exact:

This formula describes the (obvious) idea that the most black color component keeps being the most black, and the most saturated component keeps being such too.
Obviously enough, the intermediate values are non-integer. If we can multiply and divide, the things are easy -- do the math, round to nearest integer and you're done. If we can't or we don't want to multiply and divide, however, other approaches must be explored.
Let's play a little with the formula and try to get rid of the division:
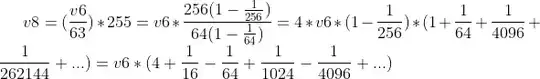
Now we can see, that the second OP's option (that is, v8=(v6<<2)+(v6>>4)), corresponds to the first two terms in the infinite expansion without round to nearest, the same as @Raffzahn proposal.
However, taking more terms and doing proper round to nearest would make the conversion more accurate. To demonstrate that, here's a simple C program doing conversions within several different numbers of terms:
#include <stdio.h>
#include <math.h>
double exact(int v6)
{
return ((double)v6)*255.0/63.0;
}
double shr6(int v6)
{
return (double)((v6<<2) + (v6>>4));
}
double t3(int v6)
{ // implements v6<<2 + v6>>4 - v6>>6 then round to nearest
return (double)(((v6<<8) + (v6<<2) - v6 + 32)>>6);
}
double t4(int v6)
{ // implements v6<<2 + v6>>4 - v6>>6 + v6>>10 then round to nearest
return (double)(( (v6<<12) + (v6<<6) - (v6<<4) + v6 + 512 )>>10);
}
void main(void)
{
double err_shr6=0, err_t3=0, err_t4=0;
for(int v6=0;v6<64;v6++)
{
double r_exact = exact(v6);
double r_shr6 = shr6 (v6);
double r_t3 = t3 (v6);
double r_t4 = t4 (v6);
printf("v6=%2d, exact=%7.3f, shr6=%5.1f, t3=%5.1f, t4=%5.1f\n", v6, r_exact, r_shr6, r_t3, r_t4);
err_shr6 += (r_exact-r_shr6)*(r_exact-r_shr6);
err_t3 += (r_exact-r_t3 )*(r_exact-r_t3 );
err_t4 += (r_exact-r_t4 )*(r_exact-r_t4 );
}
printf("shr6 mean squared error: %f\n", sqrt(err_shr6/64.0));
printf("t3 mean squared error: %f\n", sqrt(err_t3 /64.0));
printf("t4 mean squared error: %f\n", sqrt(err_t4 /64.0));
}
Its output is:
v6= 0, exact= 0.000, shr6= 0.0, t3= 0.0, t4= 0.0
v6= 1, exact= 4.048, shr6= 4.0, t3= 4.0, t4= 4.0
v6= 2, exact= 8.095, shr6= 8.0, t3= 8.0, t4= 8.0
v6= 3, exact= 12.143, shr6= 12.0, t3= 12.0, t4= 12.0
v6= 4, exact= 16.190, shr6= 16.0, t3= 16.0, t4= 16.0
v6= 5, exact= 20.238, shr6= 20.0, t3= 20.0, t4= 20.0
v6= 6, exact= 24.286, shr6= 24.0, t3= 24.0, t4= 24.0
v6= 7, exact= 28.333, shr6= 28.0, t3= 28.0, t4= 28.0
v6= 8, exact= 32.381, shr6= 32.0, t3= 32.0, t4= 32.0
v6= 9, exact= 36.429, shr6= 36.0, t3= 36.0, t4= 36.0
v6=10, exact= 40.476, shr6= 40.0, t3= 40.0, t4= 40.0
v6=11, exact= 44.524, shr6= 44.0, t3= 45.0, t4= 45.0
v6=12, exact= 48.571, shr6= 48.0, t3= 49.0, t4= 49.0
v6=13, exact= 52.619, shr6= 52.0, t3= 53.0, t4= 53.0
v6=14, exact= 56.667, shr6= 56.0, t3= 57.0, t4= 57.0
v6=15, exact= 60.714, shr6= 60.0, t3= 61.0, t4= 61.0
v6=16, exact= 64.762, shr6= 65.0, t3= 65.0, t4= 65.0
v6=17, exact= 68.810, shr6= 69.0, t3= 69.0, t4= 69.0
v6=18, exact= 72.857, shr6= 73.0, t3= 73.0, t4= 73.0
v6=19, exact= 76.905, shr6= 77.0, t3= 77.0, t4= 77.0
v6=20, exact= 80.952, shr6= 81.0, t3= 81.0, t4= 81.0
v6=21, exact= 85.000, shr6= 85.0, t3= 85.0, t4= 85.0
v6=22, exact= 89.048, shr6= 89.0, t3= 89.0, t4= 89.0
v6=23, exact= 93.095, shr6= 93.0, t3= 93.0, t4= 93.0
v6=24, exact= 97.143, shr6= 97.0, t3= 97.0, t4= 97.0
v6=25, exact=101.190, shr6=101.0, t3=101.0, t4=101.0
v6=26, exact=105.238, shr6=105.0, t3=105.0, t4=105.0
v6=27, exact=109.286, shr6=109.0, t3=109.0, t4=109.0
v6=28, exact=113.333, shr6=113.0, t3=113.0, t4=113.0
v6=29, exact=117.381, shr6=117.0, t3=117.0, t4=117.0
v6=30, exact=121.429, shr6=121.0, t3=121.0, t4=121.0
v6=31, exact=125.476, shr6=125.0, t3=125.0, t4=125.0
v6=32, exact=129.524, shr6=130.0, t3=130.0, t4=130.0
v6=33, exact=133.571, shr6=134.0, t3=134.0, t4=134.0
v6=34, exact=137.619, shr6=138.0, t3=138.0, t4=138.0
v6=35, exact=141.667, shr6=142.0, t3=142.0, t4=142.0
v6=36, exact=145.714, shr6=146.0, t3=146.0, t4=146.0
v6=37, exact=149.762, shr6=150.0, t3=150.0, t4=150.0
v6=38, exact=153.810, shr6=154.0, t3=154.0, t4=154.0
v6=39, exact=157.857, shr6=158.0, t3=158.0, t4=158.0
v6=40, exact=161.905, shr6=162.0, t3=162.0, t4=162.0
v6=41, exact=165.952, shr6=166.0, t3=166.0, t4=166.0
v6=42, exact=170.000, shr6=170.0, t3=170.0, t4=170.0
v6=43, exact=174.048, shr6=174.0, t3=174.0, t4=174.0
v6=44, exact=178.095, shr6=178.0, t3=178.0, t4=178.0
v6=45, exact=182.143, shr6=182.0, t3=182.0, t4=182.0
v6=46, exact=186.190, shr6=186.0, t3=186.0, t4=186.0
v6=47, exact=190.238, shr6=190.0, t3=190.0, t4=190.0
v6=48, exact=194.286, shr6=195.0, t3=194.0, t4=194.0
v6=49, exact=198.333, shr6=199.0, t3=198.0, t4=198.0
v6=50, exact=202.381, shr6=203.0, t3=202.0, t4=202.0
v6=51, exact=206.429, shr6=207.0, t3=206.0, t4=206.0
v6=52, exact=210.476, shr6=211.0, t3=210.0, t4=210.0
v6=53, exact=214.524, shr6=215.0, t3=214.0, t4=215.0
v6=54, exact=218.571, shr6=219.0, t3=219.0, t4=219.0
v6=55, exact=222.619, shr6=223.0, t3=223.0, t4=223.0
v6=56, exact=226.667, shr6=227.0, t3=227.0, t4=227.0
v6=57, exact=230.714, shr6=231.0, t3=231.0, t4=231.0
v6=58, exact=234.762, shr6=235.0, t3=235.0, t4=235.0
v6=59, exact=238.810, shr6=239.0, t3=239.0, t4=239.0
v6=60, exact=242.857, shr6=243.0, t3=243.0, t4=243.0
v6=61, exact=246.905, shr6=247.0, t3=247.0, t4=247.0
v6=62, exact=250.952, shr6=251.0, t3=251.0, t4=251.0
v6=63, exact=255.000, shr6=255.0, t3=255.0, t4=255.0
shr6 mean squared error: 0.345033
t3 mean squared error: 0.287384
t4 mean squared error: 0.286086
You can play with it interactively here: https://godbolt.org/z/sMr5azYM8
From the results we see that:
- The "shr6" method, that is, (v6<<2)+(v6>>4) gives the worst results,
- "t3", the three-terms method with explicit round-to-nearest is significantly better,
- "t4", four-term method, gives exact integer result.
The similar approach could be used for any other conversions of color depth.

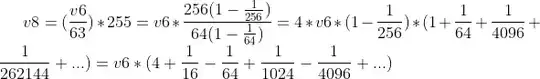
mulbut probably slower today. I'm not an engineer or mathematician but it felt like the right solution and results were great. – hippietrail Jul 28 '23 at 04:048_bit= (6_bit << 2) | (6_bit >> 4);- this makes 0 map to 0 and 63 to 255. Isn't this good enough? – Thorbjørn Ravn Andersen Jul 28 '23 at 11:22