How to implement the CCH gate in quantum computers available in clouds?

Question

How to implement CCH gate in quantum computers available in clouds? If there is not any gate directly available for it, what are the possible ways to represent CCH?

Answer 1

Assuming you've got Toffoli and single-qubit rotations, you can implement the following:

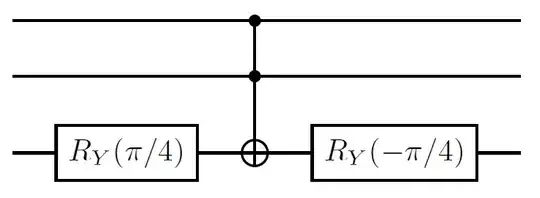
This basically works because if either of the controls is not $|1\rangle$, the Toffoli does nothing and the two single-qubit unitaries cancel each other. Whereas, if both controls are $|1\rangle$, then the net gate on the target qubit is $$ (\cos\frac{\pi}{8}I+i\sin\frac{\pi}{8}Y)X(\cos\frac{\pi}{8}I-i\sin\frac{\pi}{8}Y)=X(\cos\frac{\pi}{4}I-i\sin\frac{\pi}{4}Y)=\frac{X+Z}{\sqrt2}=H. $$

Answer 2

A brute force solution :). You can also obtain CCH via qiskit's basic gates with help of get_controlled_circuit method.

from qiskit import *
from qiskit.aqua.utils.controlled_circuit import get_controlled_circuit

q_reg = QuantumRegister(3, 'q')
qc_h = QuantumCircuit(q_reg)
qc_ch = QuantumCircuit(q_reg)
qc_cch = QuantumCircuit(q_reg)

qc_h.h(q_reg[0])

qc_ch += get_controlled_circuit(qc_h, q_reg[1])

qc_cch += get_controlled_circuit(qc_ch, q_reg[2])

print(qc_cch.qasm())

Note that it may be not the optimal gate set for representing the $CCH$ gate, because get_controlled_circuit, how I understand, doesn't optimize the obtained gate set. Also, just info, $H = u2(0, \pi)$, where $u2$ is one of the basis gates of qiskit:

$$ u2(\phi, \lambda) = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & -e^{i \lambda} \\ e^{i\phi} & e^{i(\phi + \lambda)} \end{pmatrix} $$