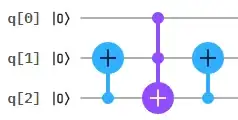
Inspired by a question Toffoli using Fredkin, I tried to do "inverse" task, i.e. to implement Fredkin gate (or controlled swap). In the end I implemented it with three Toffoli gates.
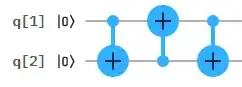
Firstly, I started with swap gate without control qubit which is implemented with CNOTs followingly:
Then I realized that I need control qubit, or in other words that I have to control each CNOT gate. As controlled CNOT is Toffoli gate (CCNOT gate), I came to this circuit
As matrix representation of Toffoli gate controlled by qubits $|q_0\rangle$ and $|q_1\rangle$ is \begin{equation} CCNOT_{01} = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ \end{pmatrix} \end{equation}
matrix of Toffoli gate controlled by qubits $|q_0\rangle$ and $|q_2\rangle$ is \begin{equation} CCNOT_{02} = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ \end{pmatrix} \end{equation}
and finnaly, matrix of Fredking gate is \begin{equation} F = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{pmatrix} \end{equation}
Since $F=CCNOT_{01} CCNOT_{02} CCNOT_{01}$, the circuit is designed corectly.
Unfortunatelly, implementation of Toffoli gate requires many CNOT gates and single qubit rotation gates.
My question: Is this implementation of Fredkin gate the most efficient one?