How powerful would quantum computers be if we had direct access to the full state vector?

Question

The state vector is exponential in size, so we can manipulate an exponential quantity of information with a linear quantity of gates. However, this doesn't give us general exponential speedup because we can only extract $n$ bits of information from an $n$-qbit system via measurement. How powerful would quantum computers be if we could actually directly access the state vector, though? Would they be equivalent in power to a nondeterministic TM?

Answer 1

How powerful would quantum computers be if we could actually directly access the state vector, though?

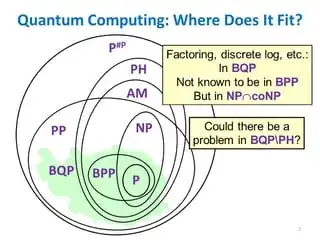
Extremely powerful! Having direct state access to the state vectors would be equivalent to having a black box that takes a quantum circuit of your choice as input and tells you any amplitude of your choice to (say) polynomially many bits of precision. The relevant complexity class, in this case, is $\mathsf{P}^{\#\mathsf{P}}$ (= $\mathsf{P}^{\mathsf{PP}}$) i.e., you'll get a polynomial-time machine with a $\#\mathsf{P}$ oracle. This follows from the fact that computing quantum amplitudes is a $\#\mathsf{P}$-complete problem (see eg. Bernstein-Vazirani and Fenner-Green-Homer-Pruim). You'll find a summary here (PDF). Thanks to Prof. Scott Aaronson for providing me the wonderful references. Nevertheless, this implies such a quantum computer would be able to solve all problems in the polynomial hierarchy and by extension all problems in $\mathsf{NP}$ and $\mathsf{coNP}$, as well as all problems in $\mathsf{PP}$, while an ordinary quantum computer is supposed to efficiently solve only $\mathsf{BQP}$ problems. You might find the following diagram useful. $\mathsf{BQP}$ is the region shaded in green.

                                            

Would they be equivalent in power to a non-deterministic TM?

                                            

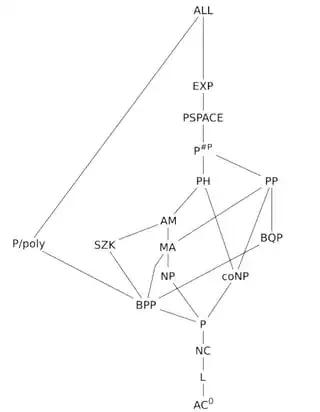
Note that $\mathsf{P}^{\mathsf{PP}}$ contains $\mathsf{PH}$ (by Toda's theorem), and $\mathsf{P}^{\mathsf{PP}}$ in turn is contained in $\mathsf{PSPACE}$. Both $\mathsf{PH}$ and $\mathsf{PSPACE}$ are describable in terms of polynomial-time alternating Turing machines ^{1, 2}. Thus, such a machine with "direct state access" would indeed be as powerful as a polynomial-time non-deterministic Turing machine (in particular, a polynomial-time alternating Turing machine).

^{1: $\mathsf{PH}$ is the set of decision problems solvable in polynomial time on an alternating Turing machine with $k$ alternations starting in an existential (respectively, universal) state.}

^{2: $\mathsf{PSPACE}$ is the set of problems decidable by an alternating Turing machine in polynomial time, sometimes called $\mathsf{APTIME}$ or $\mathsf{AP}$. ($\mathsf{PSPACE} = \mathsf{AP}$ due to [CKS81].)}

---

^{There's another related concept that you might find interesting. If you have a quantum computer that allows non-collapsing measurements along with intermediate collapsing measurements, then you then get a $\mathsf{PDQP}$ machine which can efficiently solve the Graph Isomorphism and Approximate Shortest Vector problems, unlike ordinary quantum computers. It can also search an unstructured $N$-element list in $\mathcal{O}(N^{1/3})$ time (but no faster than $\Omega(N^{1/4})$, and hence it cannot solve $\mathsf{NP}$-hard problems). For reference, check out The space "just above" BQP by Aaronson et al. (2014). It can be shown that $\mathsf{PDQP}$ does not contain $\mathsf{NP}$ relative to an oracle. Also, while $\mathsf{PDQP}$ machines can solve problems in $\mathsf{SZK}$ in polynomial-time, it cannot efficiently solve all problem in $\mathsf{NP}$. Hence, such a machine would be less powerful than a non-deterministic Turing machine.}