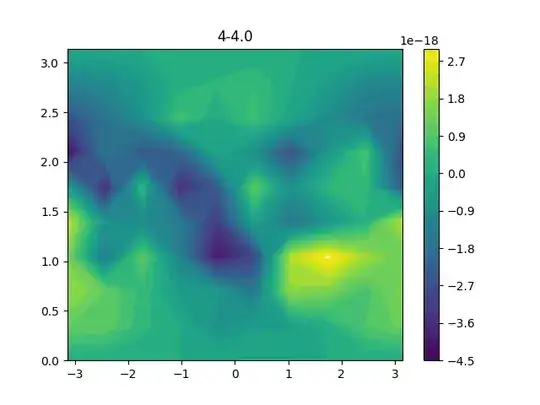
I am trying to simulate a system of j qubits and for visualization of the dynamics considering the Husimi distribution of the state.
To carry out the projection onto coherent states I have proceeded in the following manner
R=LA.expm(1j*theta*(Sx*np.sin(phi)-Sy*np.cos(phi)))
alpha=dot(R,psi0)
Where alpha represents the coherent state centered at (phi,theta), R is Rotation matrix, psi_0 spin state of |j,j> and Sx,Sy are spin operators along x and y direction respectively.
I am using scipy's linalg library to carry out exponentiation of matrix.
From all such alpha's I am able to construct the coherent distribution.
I am able to produce supposedly correct distribution for most cases but for some cases, I am getting negative values which should not be obtained for Husimi distribution, though the order of these are very less and might be related to an error in numerical approximation.
I am doubtful about my implementation and would like to clarify if the methodology that I have followed is correct or is there any better alternative for the same.