How to calculate pseudo-threshold of the [[5,1,3]] code analytically to match simulation?

Question

In this answer there is a simple method given to compute the "worst case pseudo-threshold" of the Shor code. I want to apply this to the $[[5,1,3]]$ perfect code. Namely, given a depolarizing channel (where the probability that $X$, $Y$ ,or $Z$ happens is $p/3$ and the probability that $I$ happens is $1-p$) we can compute the probability of a logical error as $$ p_L^\text{worst-case} = 1-( (1-p)^5 + 5 p (1-p)^4). $$ Basically the reasoning is that because the code has distance $d=3$ we can correct weight-0 errors (which happen with probability $(1-p)^5$) and we can correct weight-1 errors (which happen with probability $p(1-p)^4$ and there are 5 of them). Then we take the complement to find the probability of a logical error.

However, this is a "worst-case" calculation because it assumes anytime we get an error above weight-1 the code fails, which isn't necessarily true (as mentioned in this answer to my previous question).

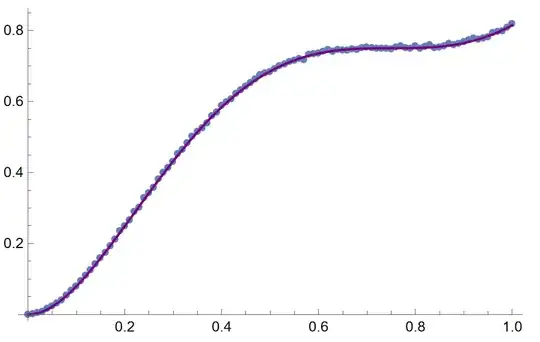
On the other hand (and mentioned in the previous question) we can try to find $p_L$ by simulating the decoding of the $[[5,1,3]]$ code in Mathematica (I used 30000 trials because it seemed smooth enough). I have plotted the probability of a logical error (y-axis) vs probability of a physical error $p$ (x-axis) for both $p_L^\text{worst-case}$ (red) and $p_L^\text{simulation}$ (blue) below. We clearly see that $p_L^\text{worst-case}$ approximates $p_L^\text{simulation}$ pretty well for small values of $p$ but deviates significantly for higher values of $p$.

I am interested in analytically deriving $p_L$ (the blue line) from first principles.

Answer 1

To find an exact expression for the blue line you could one by one check for each physical error if it leads to a logical error. For a five qubit code with a code capacity noise model this is doable as there are $4^5 = 1024$ different errors (smaller than your number of trials).

For analytically calculating the pseudo-threshold I expect you can get close by checking up to weight 2 errors.

---

Examples of some high weight errors that are correctable:

• Errors that are a stabilizer and act as the identity.
• Weight 3 errors that are stabilizer equivalent to weight one errors.

Answer 2

In accordance with what @Peter-Jan said, what I was failing to understand is that if an error is "within weight-1" of a stabilizer element then it is correctable. For example suppose the weight-5 error $E = XZZXY$ occurs. We can decompose this error as $$ XZZXY = IIIIY \cdot XZZXI. $$ The element $XZZXI$ is in the stabilizer and so it won't affect the codewords and so this error is equivalent to the weight-1 error $IIIIY$, which we can correct because the code has distance $3$.

As suggested, I went into Mathematica and figured out which errors were correctable (those that are within a weight-1 error of a stabilizer element). We get the following table.

\begin{array} {|c|c|}\hline \text{Weight} & \text{Num Correctable Errors} & \text{Num Total Errors} \\ \hline 0 & 1 &1 \\ \hline 1 & 15 &15 \\ \hline 2 & 0 & 90\\ \hline 3 & 60 & 270 \\ \hline 4 & 135 & 405 \\ \hline 5 & 45 & 243\\ \hline \end{array}

Then the probability of logical error is $$ p_L = 1 -( (1-p)^5 + 15 (p/3)(1-p)^4 + 60 (p/3)^3 (1-p)^2 + 135 (p/3)^4(1-p) + 45 (p/3)^5 ). $$

If we plot this on top of the simulated data points we get the following figure (where the purple line is $p_L$). So we see that this is the correct probability of logical error.

We can also compute the pseudo-threshold (or breakeven point) by setting $p_L = p$. We find that $p_{th} = \frac{3-\sqrt{6}}{4} \approx 0.137628$ which is an improvement over the "worst-case" pseudo-threshold of $0.131123$.