Intuition behind observable rotations during magic state injection

Question

Cleaner magic states with hook injection writes that the ZZ rotation performed amounts to a rotation of the logical $X$ observable. This is similar to High-Fidelity Magic-State Preparation with a Biased-Noise Architecture which they cite which also uses a ZZ rotation to perform this injection.

But, it's not clear to me how to think about either of these injections mathematically -- i.e., what are the formulas that govern the evolution of the logical observable? I have two questions:

1. How can we rotate the logical observable / what's the math behind this process?
2. What's the math behind this injection? It's not clear to me where the distance 2 surface code lies during evolution and why we don't need to post-select on the ZZ rotation; it seems like the hook injection of $RZ(\theta)$ could yield $RZZ(-\theta)$ on the other two states if a $-1$ is measured in the measurement ancilla.

Answer 1

One way to rotate a multi-term observable is to temporarily xor each of the terms onto an ancilla qubit, and phase the ancilla qubit, like this:

If that ZZ term is one of the observables of a logical qubit, this is applying a rotation to that logical qubit. (A more extreme version of rotating a logical qubit would be swap the logical qubit's value for a physical qubit's value, rotate the physical qubit, then swap back.)

If you look at the circuit for a distance 2 surface code, with an S gate added on the middle measurement qubit halfway through the cycle, you see it looks a whole lot like the start of the above ZZ rotation circuit:

Although the end of the circuit looks different, the S gate is in fact performing the same function as the phase gate in the ZZ rotation circuit.

By orienting the hook error the wrong way, the ZZ rotation that this S gate is performing lines up with the ZZ product that is the logical Z observable of the patch. And so it rotates the encoded surface code qubit.

Another way of seeing that it works is to realize that, by tracking a product of stabilizers prepared by reset gates through the circuit, you end up with a stabilizer equal to the logical Y of the surface code. All the data qubits were initialized in the X basis, so you would have expected to prepare logical X not logical Y. You'd need an S gate to rotate logical X into logical Y... which is exactly what the S gate in the middle of the circuit did to the logical qubit.

This screenshot from crumble is showing the Y logical observable forming from the product of resets:

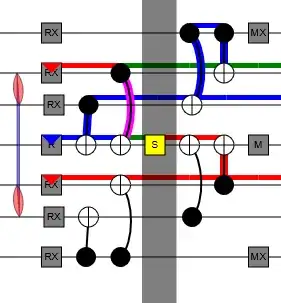
Once you understand why it works at distance 2, and how to expand a patch from distance 2 to bigger distances, the remaining work is to realize that the distance 2 injection can largely be overlapped with the patch expansion such that everything finishes in 1 round instead of 2 rounds.