This is a sequel to How are two different registers being used as "control"?
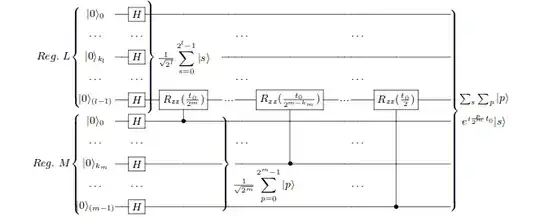
I found the following quantum circuit given in Fig 5 (page 6) of the same paper i.e. Quantum Circuit Design for Solving Linear Systems of Equations (Cao et al.,2012).
In the above circuit $R_{zz}(\theta)$ is $\left(\begin{matrix}e^{i\theta} & 0 \\ 0 & e^{i\theta}\end{matrix}\right)$
Frankly, I've no chance of getting there because there's an earlier step that I don't understand: the output on registers $L, M$ after Figure 5. The circuit diagram and the claimed output don't match up (the claimed output being separable between the $L$ and $M$ registers, when qubit $l−1$ of register $L$ should be entangled with those of register M.
I understand that after the Walsh-Hadamard transforms the state of register $L$ is $$\frac{1}{\sqrt{2^l}}\sum_{s=0}^{2^l-1}|s\rangle$$
and that of register $M$ is
$$\frac{1}{\sqrt{2^m}}\sum_{p=0}^{2^m-1}|p\rangle$$
But after that, I'm not exactly sure how they're applying the $R_{zz}$ rotation gates to get to $$\sum_s\sum_p|p\rangle \exp(i p/2^m t_0)|s\rangle$$
Firstly, are all the $R_{zz}$ gates acting on a single qubit i.e. the $l-1$th qubit in the register $L$? (Seems so from the diagram, but I'm not sure).
Secondly, it would be very helpful if some can write down the steps for how're they're getting to $\sum_s\sum_p|p\rangle \exp(i p/2^m t_0)|s\rangle$ using the controlled rotation gates.