I was wondering if something like this is possible in QISKit: let's say we have two registers containing target and ancilla qubits:
$a_0$ -------------------
$a_1$--------------------
$\vdots$
$a_4$ ------------------
$t_0$ ------------------
$t_1$ ------------------
$\vdots$
$t_4$ ------------------
These two registers are stored in one quantum register qr. So to access $a_0$ we would type qr[0], to access $a_1$ - qr[1], ..., for $t_5$ - qr[9]. We can pass this quantum register as an argument to some function:
foo(qr, ...)
What I want to do is to interleave the ancilla and target qubits:
$a_0$ -------------------
$t_0$--------------------
$\vdots$
$a_i$ ------------------
$t_i$ ------------------
$\vdots$
$a_4$ ------------------
$t_4$ ------------------
so to access $a_0$ I would type qr[0], for $t_1$ - qr[1] and so on. Finally, I would like to pass such changed quantum register qr' again as an argument to some function
foo(qr', ...)
and in this function I would like to use these changed indices. Is this possible? Other solution I figured out was to pass array of indices for ancilla and target qubits, but I would like to avoid that. Another option would be to use swap gates on these qubits


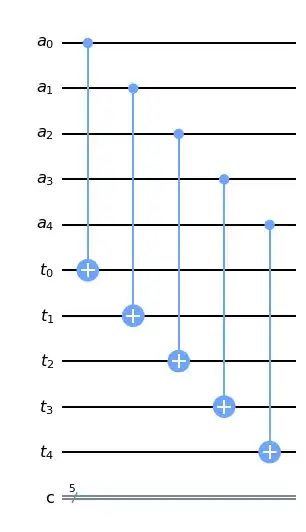
![a[i] qubit is preceeded by t[i]](../../images/8552f647d8b5b1aa644cdaf01e618250.webp)