Why isn't $Ry(\pi/2)$ gate equivalent to Hadamard gate?

Question

I've been experimenting with quantum circuits and can't quite fathom how the difference between states comes together.

Speaking in terms of simulations using qiskit, the following code yelds the same results:

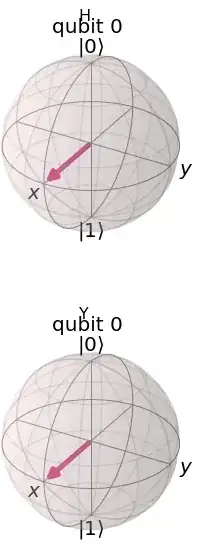
circuit = QuantumCircuit(1)
circuit.h(0)
state = Statevector.from_instruction(circuit)
display(plot_bloch_multivector(state, title="H", reverse_bits=False))
circuit = QuantumCircuit(1)
circuit.ry(0.5*np.pi,0)
state = Statevector.from_instruction(circuit)
display(plot_bloch_multivector(state, title="Y", reverse_bits=False))

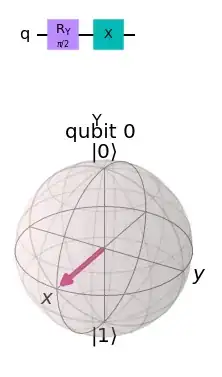
According to this page, the H-Gate is equivalent to the following circuit:

The state vector remains the same, which makes sense as it's only rotating around the x-axis.

Even negating the initial qubit state and make it a $|1\rangle$ does not bring any difference to the table.

So, I went deeper and looked at the maths behind it. Applying the H gate to $|0\rangle$ results in:

$$ H|0\rangle =\ \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} =\ \begin{pmatrix}\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}\end{pmatrix} =\ \frac{|0\rangle + |1\rangle}{\sqrt{2}} =\ |+\rangle $$

Now, using the RY-Gate, we can construct a matrix using $\frac{\pi}{2}$. This is where my understanding of the mathematical application stops tho, and I can't quite figure out how to do the rest of the calculation. This is as far as I've come, but I can't quite "translate" the result into a comparable qubit state:

$$ \begin{pmatrix} \cos(\frac{\pi}{4}) & -\sin(\frac{\pi}{4})\\ \sin(\frac{\pi}{4}) & \cos(\frac{\pi}{4}) \end{pmatrix}|0\rangle =\ \begin{pmatrix} 0.707 & -0.707\\ 0.707 & 0.707\end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} =\ \begin{pmatrix} 0.707 \\ 0.707 \end{pmatrix} $$

Reason for this question is that I am trying different circuits to classify IRIS for comparison, and I am seeing much better accuracy when using my basic Y-Rotation based circuit in comparison to qiskits ZZFeature and RealAmplitudes circuit.

Interesting that $\ket{0}$ works in the preview window but not in the post itself? — Ricardo, Oct 24 '21 at 11:20
The issue with ket happens to me sometimes. What is even worse, \ket works usually fine with other SE sites, but not the one where you need them the most, here in QC SE! you can still write them as | and langle or range — user206904, Oct 24 '21 at 13:52

Martin Vesely · Accepted Answer · 2021-10-24T20:57:27.097

14

While Hadamard gate is defined as $$ H= \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}, $$ $y$-rotation by $\pi/2$ leads to gate $$ Ry(\pi/2)= \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & -1 \\ 1 & 1 \end{pmatrix}. $$ So, there is a difference in position of -1 in the second column. Application of the $X$ gate returns the -1 in $Ry(\pi/2)$ to right place to obtain Hadamard gate.

You can easily see that $H|0\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)$ and $Ry(\pi/2)|0\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)$. Application of $X$ after $Ry$ leads to the same quantum state.

However, while $H|1\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)$, $Ry(\pi/2)|1\rangle = \frac{1}{\sqrt{2}}(-|0\rangle + |1\rangle)$. Application of $X$ after $Ry$ switches states $|0\rangle$ and $|1\rangle$ and leads to $XRy(\pi/2)|1\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)$.

This all means that $XRy(\pi/2)=H$.

edited Oct 24 '21 at 20:57

answered Oct 24 '21 at 17:15

Martin Vesely

13,891
4
28
65

1

You cannot neglect the $X$ even if you choose to ignore the global phase. Consider that $\sqrt2 H\begin{bmatrix}a\b\end{bmatrix} = \begin{bmatrix}a+b\a-b\end{bmatrix}$ and $\sqrt2 R_y(\pi/2)\begin{bmatrix}a\b\end{bmatrix} = \begin{bmatrix}a-b\a+b\end{bmatrix}$ which in general differ by more than just the global phase. The reason that it looked like the difference is in global phase only is that $|+\rangle$ and $|-\rangle$ just happen to be the eigenstates of $X$. So the last paragraph could use an update. The rest LGTM. – Adam Zalcman Oct 24 '21 at 18:49
Could you elaborate on how you went from $RY(\frac{\pi}{2})$ to that matrix? Seems as if I am missing a key step there – Ricardo Oct 24 '21 at 18:51
1

@AdamZalcman: Thanks Adam, you are absolutely right. We can neglect the global phase only in case it is involving in all basis states, i.e. the whole matrix is multiplied by some, generally complex, number. – Martin Vesely Oct 24 '21 at 21:01
@Redimo: What do you mean by that matrix? If it is relation $H = XRy(\pi/2)$ you can try to verify it by direct multiplication of matrices on the right side and comparison with $H$. – Martin Vesely Oct 24 '21 at 21:02
Ah, my bad, should've specified. The specific way you get from:
$$ Ry(\frac{\pi}{2}) =\ \begin{pmatrix} \cos(\frac{\pi}{4}) & -\sin(\frac{\pi}{4})\ \sin(\frac{\pi}{4}) & \cos(\frac{\pi}{4}) \end{pmatrix} =\ ?? =\ \frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1 \ 1 & -1 \end{pmatrix} $$
– Ricardo Oct 25 '21 at 07:16
1

@Redimo: calculated sinus and cosinus values, then factored out the $\frac{1}{\sqrt{2}}$ and finally multiplied by $X$ from left side. This proves the equivalence of Hadamard gate and $XRy(\pi/2)$. – Martin Vesely Oct 25 '21 at 09:29
1

Oh wow, that went right over my head. Thanks a lot! – Ricardo Oct 25 '21 at 09:42

score 5 · Answer 2 · answered Jul 09 '23 at 22:40

The algebraic comparison of the operations is, of course, correct.

Additionaly, noting that $H$ is Hermitian, we see that $R_y\left(\frac{\pi}{2}\right)$ is not Hermitian, and must be transformed.

A more intuitive approach is to examine the effect of the rotations on the Bloch sphere. Note that the H gate is a rotation about an axis which is on the X-Z plane, in the middle between the X and Z axes, as shown:

When we perform a 90° rotation about the Y axis, $R_y\left(\frac{\pi}{2}\right)$:

We seem to have the correct result, namely $|0\rangle\rightarrow|+\rangle,|1\rangle\rightarrow|-\rangle$.

However, on closer inspection, we see that the original x axis is now pointing "down", whereas the H gate results in the x axis pointing up ($|+\rangle$ changing places with $|0\rangle$).

Moreover, if we apply $R_y\left(\frac{\pi}{2}\right)$ again, we get the wrong result: $|+\rangle \rightarrow |1\rangle$ instead of $|0\rangle$, and $|-\rangle \rightarrow |0\rangle$ instead of $|1\rangle$

Adding a $\pi$ rotation about the X axis, $R_x\left(\pi\right)=X$, "fixes" the resulting location of the X axis (pointing "up"), making the resulting operation correct (no effect on the $|+\rangle,|-\rangle$ states which are on the X axis, and flipping the $|0\rangle, |1\rangle$ states)

Great answer, thanks! Could you give a quick summary on what the blue and red arrows represent in your bloch sphere? They look like an interesting visualization setup — Ricardo, Jul 11 '23 at 05:57
@Ricardo, they are just visual aids. The Hadamard gate is a rotation that is performed in the same direction - counter-clock-wise. looking at the left picture, we see that half the rotation (red arrows = $\pi/2$ rotation) transforms $|0\rangle$ to $|+\rangle$, the blue arrows are the other half of rotation. Thus we see that H is its own inverse. Similarly, for the right picture - $|1\rangle \leftrightarrow |-\rangle$ — inq, Jul 11 '23 at 13:42

score 3 · Answer 3 · answered Oct 25 '21 at 12:55

Just to emphasise the point on the accepted answer...

The two gates, when applied to a specific state, give the same output. That does not mean they are the same, because the action on another state may be different (and I don't just mean a global phase).

For example, if you take the state $|+\rangle=(|0\rangle+|1\rangle)/\sqrt{2}$ then $$ H|+\rangle=|0\rangle, $$ but $$ R_Y(\pi/2)|+\rangle=|1\rangle. $$ The two outcomes are orthogonal. So, in this case, you can definitely tell which of the two you have just by measuring the output.

Why isn't $Ry(\pi/2)$ gate equivalent to Hadamard gate?

3 Answers3