1

1. On page 73 of John Watrous' famous book, a quantum channel is defined as a linear map

$$\Phi: L(\mathcal{X})\rightarrow L(\mathcal{Y})$$

Now $L(\mathcal{X})$ stands for $L(\mathcal{X},\mathcal{X})$, which is itself a collection of all linear mappings $\mathcal{A}: \mathcal{X}\rightarrow \mathcal{X}$ (page-8).

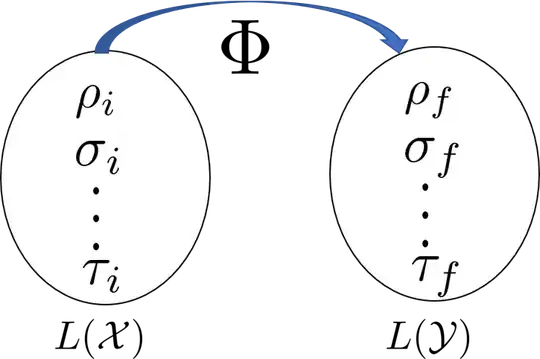
2. As a physics student, when I look at some simple examples of a quantum channel, say a phase damping channel $\Phi_{PD}$, the way I look at it is that it takes my initial state $\rho_i$ at time $t_i$ to a final state $\rho_f$ at time $t_f$.

$$\Phi_{PD} [\rho_i] \rightarrow \rho_f$$

Trying to compare these two scenarios, it seems $\rho_i \in L(\mathcal{X})$ and $\rho_f \in L(\mathcal{Y})$. What happens to $\mathcal{A}$ here? What is exactly the one-to-one correspondence between 1 and 2?

Edit: I have tried to convey my query by a diagram in which the job of $\Phi$ is illustrated. I want to understand what is $\mathcal{A}$ in the following diagram:

enter image description here

glS
  • 24,708
  • 5
  • 34
  • 108
Zubin
  • 253
  • 1
  • 6
  • 1
    What is the apparent mismatch here? A density matrix is a linear operator on a Hilbert space $\mathcal X$, in the simplest case, a pure state $\rho = |\psi\rangle\langle\psi|$. – Markus Heinrich Sep 16 '21 at 11:50
  • Can you identify $\mathcal{A}$ in 2? – Zubin Sep 16 '21 at 12:05
  • Do you mean the $A$ that you mentioned in 1? Well, $\rho_i\in L(\mathcal X)$ and the output state $\rho_f = \Phi_{PD}(\rho_i) \in L(\mathcal X)$, too (at least for phase damping channel we have $\mathcal Y = \mathcal X$). A quantum channel simply maps linear operators to linear operators. – Markus Heinrich Sep 16 '21 at 12:14
  • My point is: $\Phi$ has the domain (range) $L(\mathcal{X})$, and $\mathcal{A}$ has the domain (range) $\mathcal{X}$. If the domain (range) of $\Phi$ is the set of density matrices $\rho_i (\rho_f)$ in 2, what is $\mathcal{A}$ and what is its domain (range)? – Zubin Sep 16 '21 at 12:27
  • 1
    I see, your confusion arises because in 2) a quantum channel acts only on density matrices, but in 1) Watrous defines it to act on all linear operators, right? If I understood that correctly, I can formulate an answer shortly. – Markus Heinrich Sep 16 '21 at 12:34
  • 2
    In your item number 2, $A = \rho_i$. – John Watrous Sep 16 '21 at 12:40
  • @JohnWatrous, thank you very much for responding. That is exactly my confusion, I have always thought of $\rho_i$ as an element of set $L(\mathcal{X})$ and not a mapping/rule which takes one such element to another. – Zubin Sep 16 '21 at 12:46
  • When we think about a state $\rho$, we often think about it as a matrix rather than a linear map; and correspondingly you can think about $L(\mathcal{X})$ as simply being a set of matrices (or represented by a set of matrices) rather than a set of linear maps. But the properties of states as linear maps are important -- for example, we often care a great deal about the eigenvalues of a state $\rho$. – John Watrous Sep 16 '21 at 12:56
  • If the state $\rho$ is a linear map, what is its argument, I mean what does it act on? I understand that both $\Phi$ and $\rho_i$ can have a matrix representation and one can talk about their eigenvalues and other properties. But I think they are still different things. The state is an element of a set, and the map is a rule that takes you from one element to another. – Zubin Sep 16 '21 at 13:14
  • If $\rho\in L(\mathcal{X})$ is a density operator, it acts on elements of $\mathcal{X}$. Perhaps my answer to this question may help to explain this. – John Watrous Sep 16 '21 at 19:26

1 Answers1

1

  1. The set $\mathrm L(\mathcal X)\equiv\mathrm L(\mathcal X,\mathcal X)$ is the set of linear maps from $\mathcal X$ to $\mathcal X$. In other words, $A\in\mathrm L(\mathcal X)$ iff $A$ is a linear function of the form $A:\mathcal X\to\mathcal X$.

  2. Note that $\mathrm L(\mathcal X,\mathcal Y)$ is itself a vector space. That means you can have, for example, $\mathcal X\equiv \mathrm L(\mathcal Y,\mathcal Z)$ in the above. Quantum maps are examples of this: $\Phi\in\mathrm L(\mathrm L(\mathcal X),\mathrm L(\mathcal Y))$ means that $\Phi$ is a linear function $\Phi:\mathrm L(\mathcal X)\to\mathrm L(\mathcal Y)$. More explicitly, for any $\lambda,\mu\in\mathbb C$ (I'm assuming $\mathcal X,\mathcal Y$ to be complex vector spaces here) and $A,B\in\mathrm L(\mathcal X)$, you have $$\Phi(\lambda A+ \mu B) = \lambda \Phi(A)+\mu\Phi(B).$$ Note that in this, $A,B:\mathcal X\to\mathcal X$, meaning they are also linear functions, and thus for any $\alpha,\beta\in\mathbb C$ and $x,y\in\mathcal X$ you have $$A(\alpha x+\beta y)=\alpha A(x) + \beta A(y), \quad B(\alpha x+\beta y)=\alpha B(x) + \beta B(y).$$ To fix ideas, in the context of quantum information you typically have $A,B$ as density matrices of some quantum state, and $\lambda,\mu$ will be real scalars because $\lambda \rho$ is not a state if $\rho$ is a state and $\lambda\notin\mathbb R$.

  3. Following the above discussion, an operator $A\in\mathrm L(\mathcal X)$ can be thought of as a function $\mathcal X\to\mathcal X$, or as a vector in $\mathrm L(\mathcal X)$. Both things are true and consistent with each other. Matrices are, in general, ways to represent linear operators, so whenever you work with a matrix, you are doing exactly this.

glS
  • 24,708
  • 5
  • 34
  • 108
  • In point number 2 of your answer, if we identify $A$ and $B$ with density matrices (in the context of quantum information), what would we identify $x$ and $y$ with? I mean if the density matrix is itself a map, which objects are being mapped by it? I was always taught that the density matrices represent states and operators (and super operators) act on them. – Zubin Sep 17 '21 at 09:01
  • 1
    @Zubin if $A\equiv\rho$ is a density matrix, the vectors it acts on, your $x,y$, don't necessarily have a direct physical meaning. Though its eigenvectors/eigenvalues can be understood as the ensemble of pure states making up the density matrix. You can in general think of representing a state as an operator as a convenient mathematical tool. It doesn't necessarily mean we care about the vectors they act on. This is not so weird by the way: you e.g. represent groups as linear operators, but that doesn't mean the vectors on which these operate have themselves a direct meaning – glS Sep 17 '21 at 10:37
  • 1
    also, I should point out that you don't strictly need to represent states as density matrices. At the end of the day, you could do everything with pure states represented as (projective) vectors. But such description can get very tricky when you start considering scenarios with noise and classical uncertainties due to various sources (and once you work out the tricky aspects of it, you'd probably find out that the easier description you end up with was the density matrix formalism you wanted to avoid in the first place) – glS Sep 17 '21 at 10:39
  • 1
    @Zubin by the way, the current title is very generic, which makes the question harder to retrieve and less useful in general. Could something along the lines of "If density matrices are linear operators, what vectors do they operate on?" be a more accurate description of what you are actually asking? – glS Sep 17 '21 at 10:42
  • +1 @gIS One way to think about the restriction $\lambda, \mu\in\mathbb{R}$ is that the set $D(\mathcal{X})$ of density matrices is contained in the real vector space $\mathrm{Herm}(\mathcal{X})$ of Hermitian operators which is a subspace of the complex vector space $L(\mathcal{X})$. The hierarchy of two vector spaces consisting of complex vector space $\mathcal{X}$ and real vector space $\mathrm{Herm}(\mathcal{X})$ corresponds to the concept of Heisenberg cut since the coefficients in the former are amplitudes and in the latter probabilities. – Adam Zalcman Oct 14 '21 at 21:36