After asking on the Discord (thanks for pointing me to that Bob!), I got several proofs.
First proof (thanks Miriam Backens)
Lemma A.13, A.14 and A.15 of this paper, which contains also many interesting proofs. This method also works in the real stabiliser fragment, where Lemma A.13 is taken as a an axiom instead of the EU rule.



Second proof (thanks John van de Wetering)
First, we derive the Y-state-identity, for instance given here in appendix A (I rewrote the proof with scalars):
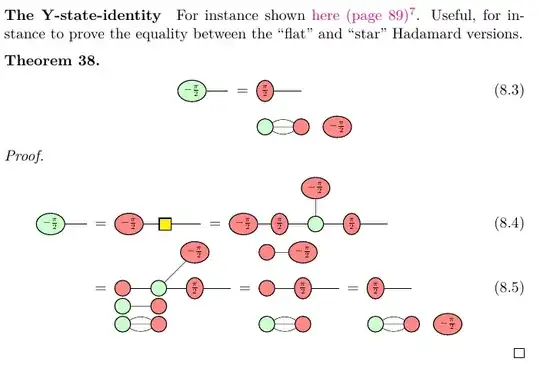
It is now trivial to derive the equivalence between the two forms of the Hadamard (it is also possible to show that the last form is true when inverting all angles by using the fact that $HH=I$):

Then, John was proposing this reduction (sorry, I've no time to write it down properly, so I shamefully copy/pasted his picture), where the Y-state identity is used in the last equation of the first line, and where the Hadamard identity is used right after, then it is the Hopf rule and the last equality can be proven using the K-rule + bialgebra + hopf (one may need also a proper analysis of scalars...):