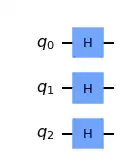
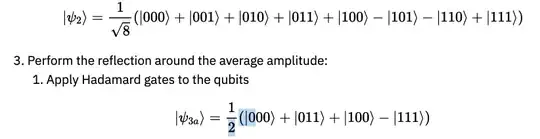Can someone shows me, step by step, how to apply Hadamard and output the result?
-
1related: https://quantumcomputing.stackexchange.com/q/14066/55 and links therein – glS Jul 22 '21 at 17:42
1 Answers
First, note that the Hadamard gate has the matrix representation as $H = \dfrac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} $. When you apply Hadamard gates to all the qubits,
what you essentially doing is applying the operation $U = H \otimes H \otimes H$ to the state $|\psi_2\rangle$. Now,
$$ H \otimes H = \dfrac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1\\ 1 & -1 \end{pmatrix} \otimes \dfrac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1\\ 1 & -1 \end{pmatrix} = \dfrac{1}{2}\begin{pmatrix} 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1 \end{pmatrix} $$
To get $ H \otimes H \otimes H $ you have to do another tensor. Thus, applying Hadamard gates to the state $|\psi_2\rangle$ can be written in term of matrix multiplication as
\begin{equation} \begin{bmatrix} \tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} \\ \tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} \\ \tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} \\ \tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} \\ \tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} \\ \tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} \\ \tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} \\ \tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & \tfrac{1}{\sqrt{8}} & -\tfrac{1}{\sqrt{8}} \\ \end{bmatrix} \begin{bmatrix}\dfrac{1}{\sqrt{8}} \\ \dfrac{1}{\sqrt{8}} \\ \dfrac{1}{\sqrt{8}}\\ \dfrac{1}{\sqrt{8}}\\ \dfrac{1}{\sqrt{8}}\\ -\dfrac{1}{\sqrt{8}} \\ -\dfrac{1}{\sqrt{8}} \\ \dfrac{1}{\sqrt{8}} \end{bmatrix} = \dfrac{1}{2} \begin{bmatrix} 1 \\ 0 \\ 0\\ 1 \\ 1 \\ 0 \\ 0 \\ -1 \end{bmatrix} \end{equation}
Now, the resulting vector above can be written in term of the ket representation as your formula $|\psi_{3a} \rangle$. That is, \begin{equation} \dfrac{1}{2} \begin{bmatrix} 1 \\ 0 \\ 0\\ 1 \\ 1 \\ 0 \\ 0 \\ -1 \end{bmatrix} = \dfrac{1}{2} \big( |000\rangle + |011\rangle + |100\rangle - |111\rangle \big) \end{equation}
- 13,822
- 2
- 10
- 30
-
-
2@pyb There are three qubits in your system because if you look at the basis states, there are 3 qubits within it. To see this more clearly, note that the state $|\psi \rangle = \dfrac{|000\rangle + |111\rangle }{\sqrt{2} } = \dfrac{|0\rangle^{\otimes 3} + |1\rangle^{\otimes 3} }{\sqrt{2} } $ is another three qubit systems. But $|\psi \rangle = \dfrac{|0000\rangle + |1111\rangle }{\sqrt{2} } = \dfrac{|0\rangle^{\otimes 4} + |1\rangle^{\otimes 4} }{\sqrt{2} } $ is a four qubit system. Now, another 4 qubits state could be: $|\psi \rangle = |0101\rangle $. – KAJ226 Jul 22 '21 at 23:20
-
thank you! Do you know of a resource that explains how to go from the $|\psi_3a\rangle$ to the Dirac notation? I know how to convert from the Dirac notation to vectors then apply linear algebra, but not the other way around. – pyb Jul 23 '21 at 01:01
-
-
1You can just look at the position of the element in the vector and convert it to binary. For instance, there is a $1$ in the first (0th) position of the vector, so this corresponds to $|000\rangle$. Then there is also a $1$ in the 3rd position of the vector. Now $3$ is binary is $011$ so this corresponds to $|011\rangle$. There is a $1$ in the 4th position, and $4$ in binary is $100$ so this corresponds to $|100\rangle$. Then there is a $1$ in the last spot, the $7th$ position, and $7$ in binary is $111$ thus the state is $|111\rangle$. put them together you have the last line :) – KAJ226 Jul 23 '21 at 04:36
-
1wow, thank you so much! It will make reviewing intro courses much easier. I miss why the 1st $1$ is encoded to |000⟩ and not |001⟩, but I will figure it out. – pyb Jul 23 '21 at 17:58
-
1This is because we start counting from $0$. $0$ corresponds to $000$. Then $1$ corresponds to $001$. – KAJ226 Jul 23 '21 at 19:35