Here is an MWE: a simple circuit on three qubits with a CNOT acting on qubits 0 and 2. The coupling map prohibits a two-qubit gate between qubits 0 and 2 and so qubit 1 must get involved.
from qiskit import QuantumCircuit
from qiskit.compiler import transpile
from qiskit.transpiler import CouplingMap
from qiskit.quantum_info import Operator
from qiskit.circuit.library import Permutation
from itertools import permutations
qc = QuantumCircuit(3)
qc.cx(0, 2)
coupling_map = CouplingMap([[0, 1], [1, 0], [1, 2], [2, 1]])
transpiled_qc = transpile(qc, basis_gates=['cx'], coupling_map=coupling_map)
Now, if I check
Operator(transpiled_qc).equiv(qc) # False
Although the resulting circuit looks reasonable
I thought that the difference between the original and the transpiled circuit might be a permutation of qubits, but the following check did not work either
for p in permutations([0, 1, 2]):
permutted_qc = qc.compose(Permutation(3, p))
print(Operator(transpiled_qc).equiv(permutted_qc)) # All False
Addition
If I fix the initial_layout in the transpilation options
transpiled_qc = transpile(qc, basis_gates=['cx'],
coupling_map=coupling_map, initial_layout=[0, 1, 2])
then the resulting circuit
is indeed equivalent to the transpiled circuit plus a permutation
permutted_qc = qc.compose(Permutation(3, [1, 0, 2]))
print(Operator(transpiled_qc).equiv(permutted_qc)) # True
My questions is now I guess -- how to be systematic about it? How to read out an appropriate permutation before trying all options (I have much more complicated circuits in mind). I mean, isn't it a basic human need to transpile a circuit and get True as a result of the equivalence test?
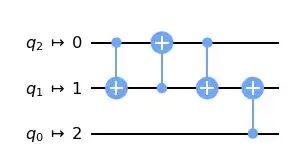
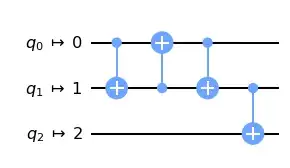


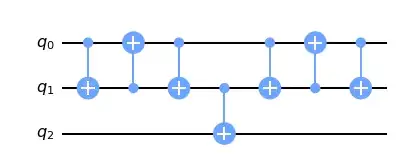
composemodifiesqc? – Yael Ben-Haim Jun 15 '21 at 07:40