12

I have seen circuits with 30 qubits and around 500 gates. Also circuits with 32 qubits and 6000 gates. Are circuits with more than 1000 gates common in quantum computing? Are there many quantum algorithms that require more than 1000 gates? How common are they?

Alejandro Arcila
  • 131
  • 5

1 Answers1

24

I'd say it's far more common for quantum algorithms to use billions of gates than thousands. And that's assuming you're ignoring Clifford gates as well as error correction overhead! If you want to count those, add in another factor of a million.

For example...

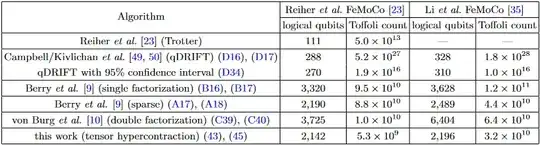
According to Table III of https://arxiv.org/abs/2011.03494 , quantum chemistry algorithms looking at properties of the FeMoCo molecule use half a billion Toffoli gates.

enter image description here

According to Table 1 of https://arxiv.org/abs/1905.09749 , factoring 2048 bit numbers takes 3 billion Toffoli gates:

enter image description here

According to Table 1 of https://arxiv.org/abs/2001.09580 , 256 bit elliptic curve discrete logarithms take a few billion T gates:

enter image description here

Craig Gidney
  • 36,389
  • 1
  • 29
  • 95
  • Wow, that's sobering. And how many gates can currently be run on a real device? – Nikita Nemkov Jun 01 '21 at 08:42
  • @WeatherReport I think Craig can give more reliable numbers than me. AFAIK, the number of gates is of the order of 100, depending on the platform. The problem is that the number of gates is limited by the gate fidelity since errors are accumulating and the outcomes eventually become white noise. You cannot increase the fidelity arbitrarily, that is why you need quantum error correction. Among others, this requires a notable overhead in the physical qubits. Current devices with 50-100 qubits can only provide a few (1-2) logical qubits with realistic codes, so you cannot do much. – Markus Heinrich Jun 01 '21 at 09:21
  • 4
    @WeatherReport Off the top of my head, the quantum supremacy experiment that google did used roughly 1500 gates and had a signal-to-noise of roughly 0.1%. So you can do classically hard things with thousands of gates, but it's a big open question if you can do useful things (as in things industry would pay for) with that many gates. The closest I know of is Scott Aaronson's client certified randomness proposal, but it rides a fine line between too-hard and too-easy due to verification being harder than spoofing (except spoofing has a strict time limit). – Craig Gidney Jun 01 '21 at 12:04
  • And to add a quantum finance example (that I am shamelessly a co-author of :P), from Table 1 in https://arxiv.org/abs/2012.03819, pricing commonly used non-trivial options (autocallables and TARFs) using Monte Carlo simulations on a quantum computer takes ~10 billion gates. – sheesymcdeezy Aug 01 '21 at 08:11
  • In the last example, the lowest number of T gates that I see is more than 10^31. How is that *a few billion*? – user1271772 No more free time Sep 03 '23 at 17:53
  • @user1271772 The base of the exponents is 2, not 10. 2^31 is roughly 2 billion. – Craig Gidney Sep 03 '23 at 19:26
  • That makes much more sense, I had first looked at the first two tables in a lot of detail, so when I arrived at the third table I was still thinking in base 10. Sorry and thanks! – user1271772 No more free time Sep 03 '23 at 22:16