2

In this example implementation of Grovers Algorithm from the Qiskit Textbook which solves a $2\times 2$ sudoku puzzle:

https://qiskit.org/textbook/ch-algorithms/grover.html

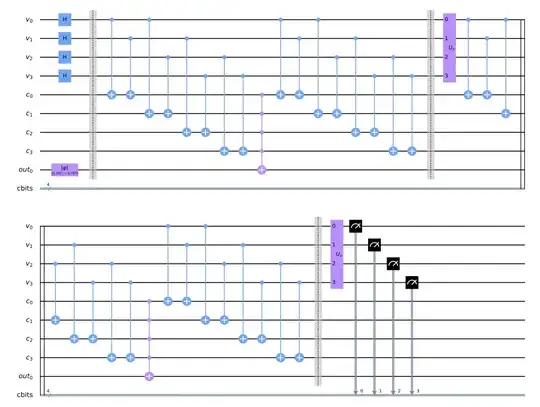
The circuit iterates twice (see picture)

My question is:

How is the data in the $c_0 - c_3$ and out0 qubits utilised.

To me it looks like $c_0 - c_3$ and out are never fed back into the $v_0 - v_3$ qubits, and $v_0 - v_3$ are the only ones that are measured at the end.

I'm not sure if I've misinterpreted how entanglement works here, or how the CX gates work.

enter image description here

glS
  • 24,708
  • 5
  • 34
  • 108
Ben
  • 23
  • 2

1 Answers1

1

The quantum register c can be regarded as ancilla. For the first part of each iteration(before the CCCC-NOT), each two cx compares if the state of the two qubits is identical, if not, one ancilla will be converted to the state $|1\rangle$. The CCCC-NOT checks whether the four ancillae are all $|1\rangle$, if so, a phase-flip operation is implemented.

The second part of each iteration(between CCCC-NOT and the diffusion unitary) converts the ancillae into its original state($|0000\rangle$, for reversibility). The action of diffusion unitary should be familiar to you.

Introduce ancilla into the quantum circuit will certainly increase the difficulty of classical simulation, but it may decrease the difficulty of designing an algorithm (sometimes it is impossible to achieve the goal without the ancilla).

Yitian Wang
  • 958
  • 4
  • 16
  • So just to be clear the ancillae and out qubit never affect the values in the v register? I understand how the out qubit will show if the answer is reached, but if we only measure the v register and never feedback to it - I struggle to see the point of the ancillae? Or have I missed a key element of entanglement? Thanks – Ben Nov 24 '20 at 22:00
  • The job of the oracle of the Grover algorithm is to append a global phase $-1$ to the state that satisfies some conditions while leaving other states unchanged. So for question 1, yes, they only affect the phase. The introduction of ancillae is to enable us to compare whether the four requirements are satisfied (so there is a CCCC-not, only if both conditions, or say, all the ancillae, are in the state $|1\rangle$ will the phase flip be appended). I don't think you are missing the entanglement, the logic here is kind of classically alike. – Yitian Wang Nov 25 '20 at 00:38
  • I think the bit I'm missing is how phase flipping the out qubit has the effect of phase flipping the whole 'winner' state of the v register so that it can be amplified. To me that out qubit seems isolated and never feeds back into the circuit. I appreciate that if it's in the |+> state we've found the correct answer, but I have no idea how that's fed back into our v register, since it's only ever a target bit and not a control. So if this were classical it would have no bearing on the output. Really appreciate the time you've taken to respond so far by the way! – Ben Nov 25 '20 at 21:40
  • This is because of the quantum entanglement, the $out_0$ qubit is entangled with other qubits and thus forms numerous 9-qubit states. If you changed the phase of a specific state when operating $out_0$ while leaving other states unchanged, then this phase can be observed at other places like $v_0$. So this $out_0$ qubit can be removed, you may have a try and see if the result is changed. – Yitian Wang Nov 26 '20 at 01:27
  • But if you remove the $out_0$ qubit and add the phase at the qubit $v_0$, instead of CCCC-NOT gate, you will need a CCCC-Phase gate, where a single-phase gate $\hat P(\theta)=\hat U_1(\theta)\hat X\hat U_1(\theta)\hat X$(https://quantumcomputing.stackexchange.com/questions/2477/phase-shift-gate-in-qiskit). The replaced operation is due to that the $out_0$ qubit is initialized beforehand while $v_0$ can not do things like that, at least if you do not want to think that hard. – Yitian Wang Nov 26 '20 at 01:34
  • That's completely clarified it! Thank you – Ben Nov 26 '20 at 07:26