0

I self-study quantitative finance, but I have a hard time connecting the textbook formula with the market reality and available data.

I use delta-gamma approximation to estimate the price change of warrants on the French market after a small change $dS$ of the underlying asset:

$P_{est} \approx P_0 + \Delta * dS + \frac12 * \Gamma * (dS)^2 $

This is an assumption based on the fact that $dS$ is small all other parameters (volatility, interest rate, ...) will remain constant. I understand that when $|dS|$ grows, the error ${err} = P_{real} - P_{est}$ grows in absolute value. But can we know for sure the sign of the error? In other words, is the estimate always wrong by excess (resp. default), or is this something we can't know?

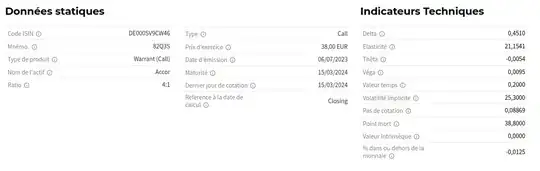
FWIW, below is an example of the typical data available for a Warrant on the emitter website. Notice the gamma isn't specified, and I have to estimate it from recent price changes (which is sub-optimal, I suppose). Techinical data for the DE000SV9CW46 warrant

Sylvain Leroux
  • 101
  • 5
  • 1
    Delta is linear to a payoff that is a convex curve (see here, so it's always below. Gamma somewhat corrects for that. To get the understanding you just can use a generic example and plot it. – AKdemy Feb 20 '24 at 10:15
  • Thanks for the reply @AKdemy. I knew the answer when using only the delta. But I wondered if the Gamma couldn't "correct" the estimated curve up to the point it would cross over the real curve. – Sylvain Leroux Feb 20 '24 at 10:19

0 Answers0