Exchanges will usually list greeks along with the option, for example this SPX call on the CBOE:
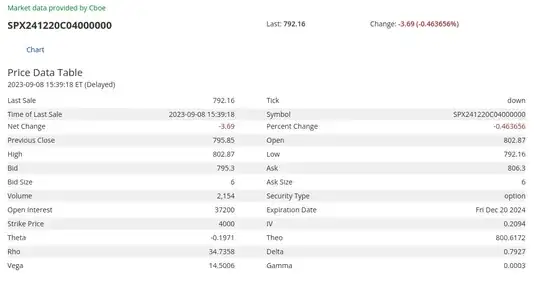
But how does the exchange calculate these greeks? I can think of a few ways to do so:
- Use the "instantaneous" values of the most recent trades (minimum number to numerically compute the derivative)
- Fit a hyperplane through a predefined amount of samples (say, minutes? hours? days? of time)
- Fit the entire trade history to a model (e.g., B-S), and derive the greeks from the model
Presently I'm primarily interested in delta and theta, and I'm wondering how much I can "trust" the greeks to predict the long-term (~months) behaviour of the option price.
If the greeks are "instantaneous" values, then they would be extremely noisy and useless for my purposes. But if they are derived from the long-term history of the option, then it would be much more reliable for me