0

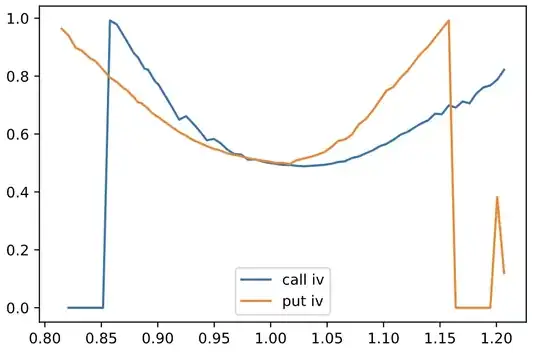
I've been analyzing Tesla stock American options data and have observed an interesting pattern that I'd appreciate some help understanding.

For this analysis, I obtained the Implied Volatilities (IVs) by reversing the Binomial Option Pricing model specific to American options and used the current market price derived via PCP at atm.

Unlike European options, where we know that the In-The-Money (ITM) Implied Volatility (IV) of the put side equals the Out-Of-The-Money (OTM) IV of the call side and vice versa, American options seem to behave differently.

In the case of American equity options, it appears to be such that:

IV of ITM Call side > OTM Put side IV of ITM Put side > OTM Call side For clarity, I've attached an image plot that illustrates this:

Tesla Implied Voltality against moneyness

While I'm aware of the fact that Put-Call Parity does not hold in American options, causing implied IVs for calls and puts to diverge, I'm struggling to understand the mathematical reasoning that leads to ITM options generally being pricier.

Could someone explain why this might be the case? Any insights into the mathematics or logic behind this observed pattern would be greatly appreciated.

Thank you.

Bob Jansen
  • 8,552
  • 5
  • 37
  • 60
Manish
  • 1
  • 1
  • It will be impossible to answer without knowing how you obtained the IV estimates. May well just be that you enter regions where early exercise is possible and European option prices would be priced lower than intrinsic value. If your vol is obtained without properly taking this into account you will have an explanation. – AKdemy May 21 '23 at 14:27
  • this is happening for each day in 2022 and for this analysis, I obtained the Implied Volatilities (IVs) by reversing the Binomial Option Pricing model specific to American options and using the current market price derived via PCP at atm. – Manish May 21 '23 at 17:07
  • How do you apply PCP with American options? Your ITM options drop of because of illiquidity, timing mismatch is a big issue (another concern will be how you handle wide bid ask spreads). Also, I think a lot will be explained by this excellent answer. Borrow costs and funding costs are very tricky. – AKdemy May 21 '23 at 19:26

0 Answers0