Call option on forward

Question

What is the trade description behind a call option on a forward? How can it be described with words and not with mathematical formulas?

So what is the intuition behind the following payoff:

$$Payoff_{1}=\max\left(F\left(T,\tilde{T}\right)-K,0\right)$$

and how does it differ from the following payoff:

$$Payoff_{2}=\max\left(S\left(T\right)-K \cdot p\left(T,\tilde{T}\right),0\right),$$

where $T$ is the call option expiry, $\tilde{T}$ is the delivery date of the underlying, $F\left(t,\tilde{T}\right)$ is the current forward price, $S\left(t\right)$ is the spot price, $p\left(t,\tilde{T}\right)$ is a zero coupon bond maturing at $\tilde{T}$ and $K$ is a strike.

The second one is the positive part of the value of a forward position...I would say this is also a call option on forward, because I would exercise the option on a forward, if the forward position value would be non-negative. ... So my main problem is that I don't understand what is the main difference between the two payoffs... But what does it mean exactly that "I have a call option on a forward"? — Kapes Mate, Dec 21 '22 at 14:11
A call option on a forward is in essence identical to any other call option - buying a call gives you to right to buy some underlying (can be a stock, a future, a forward, a commodity, an interest rate swap, ... ). I think you are confusing value (zero at initiation of a forward) with price. (the price a cash price of assets as specified in the contract). Instead of spot prices, you use the forward price - that is really the difference. — AKdemy, Dec 21 '22 at 14:32
You can have a look at this answer to see how a spot and forward option look like in FX. — AKdemy, Dec 21 '22 at 14:34
So buying a call on a forward mean, that I have the opportunity in $T$ to decide if I want to buy some underlying for $K$ at time $\tilde T$? But it also means, that at $\tilde T$ I (as a call option holder) won't necessary get a non-negative payoff, even when I exercised the option at time $T$. E.g. I decide in $T$ to exercise the option, so I will buy underlying for $K$ at $\tilde T$...but if $F(\tilde T, \tilde T)=S(\tilde T)<K$ then it is negative cash-flow for me. — Kapes Mate, Dec 21 '22 at 14:46
I’m voting to close this question because it is only a shortened version of a closed question by the same account. — Alper, Dec 21 '22 at 20:27
Closing this question was a quite passive aggressive act. It is indeed a shortened version of a closed question, but it is not a rational reason to close the current one. I honestly don't understand what is the problem with this question. ... — Kapes Mate, Dec 21 '22 at 21:31
The previous question was a long and not focused one, and when that was closed I got the suggestion to write it again, but try to ask it more professional. I think the current question is straightforward and short, and I really wanted to read a proper answer to it. Fortunately, I've already got it below. So please, next time first give me a hint how to transfer it a good question, and after close it. — Kapes Mate, Dec 21 '22 at 21:32
Your question was closed because it was just a rewriting of a previous question of yours whose closure should have been addressed through editing, not re-posting. This is explained in the article "What if I disagree with the closure of a question? How can I reopen it?" in the help center. If you disagree with any of the policies or guidance outlined in the help center, you can enquire about it in QF Meta. — Alper, Dec 22 '22 at 00:56

AKdemy · Accepted Answer · 2022-12-22T01:43:45.023

A call option on a forward is in essence identical to any other call option - buying a call gives you to right to buy some underlying (can be a stock, a future, a forward, a commodity, an interest rate swap, ... ). I think you are confusing value (zero at initiation of a forward) with price (the cash price of the asset as specified in the forward contract). Instead of spot prices, you use the forward price - that is really the difference.

The delivery date of the forward is the date when the underlying of the forward is transferred. In an option on a forward, you buy the right to buy the forward at some time T. What matters for exercising the option is what the forward price is relative to your strike -> max(F-K,0). It is the same for stock options by the way. You may receive the stock (if it is not cash settled) but it is completely independent of what the stock may be worth at some time in the future (after you exercise). In the worst case, you exercise the option on Friday because S > K but on Monday the firm goes bankrupt and your stock is now worthless. If you do not want to be exposed to changes in the price of the underlying after you exercise, you just sell the stock (or the forward - which in OTC often means you buy an offsetting position).

You can have a look at this answer to see how a spot and forward option look like in FX. This assumes that the forward expires at the exercise time.

With regards to discounting from T̃ or T

If you have a forward that expires later, you get the discounting from the expiry date (delivery date) of the forward. Everything else is identical. You can see this nicely at Matlab's website (where you can even run the code without having a license). An intuitive explanation is given on Wikipedia. It can be replicated quickly in any programming language. Below, I will use Julia.

We first need to import relevant packages, define the CDF and Black pricer. Note that T and T̃ are needed for pricing with Black on forwards where T̃ > T.

using Distributions, DataFrames, Dates
N(x) = cdf(Normal(0,1),x)
# generic Black-76 allowing for futures and forwards
function Black(F,K,T,T̃,rd,σ)
    d1 = ( log(F/K) +  0.5*σ^2*T ) / (σ*sqrt(T))
    d2 = d1 - σ*sqrt(T)
    c  = exp(-rd*T̃)*(F*N(d1) - K*N(d2))
    p  = exp(-rd*T̃)*(K*N(-d2)-F*N(-d1))
return c, p
end

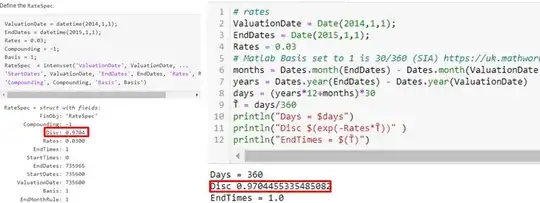
For the rates, we need to be consistent with the Matlab implementation, which uses 30/360 (SIA) in the examples on the webpage. Details for the so called Basis in the intenvset interest rate structure can be found here. EndTimes is the year fraction.

# rates
ValuationDate = Date(2014,1,1);
EndDates = Date(2015,1,1);
Rates = 0.03
# Matlab Basis set to 1 is 30/360 (SIA) https://uk.mathworks.com/help/fininst/intenvset.html#namevaluepairarguments
months = Dates.month(EndDates) - Dates.month(ValuationDate) # compute month difference
years = Dates.year(EndDates) - Dates.year(ValuationDate)
days = (years*12+months)*30
T̃ = days/360
println("Days = $days")
println("Disc $(exp(-Rates*T̃))" )
println("EndTimes = $(T̃)")

$Matlab \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; Julia$

Now, all that is left is to define the option parameters to match Matlab exactly.

# option 
Strike = (200,90) # call / put
AssetPrice = 107
Sigma = 0.28
Settle = Date(2014,1,1)
Maturity = Date(2014,10,1)
months = Dates.month(Maturity) - Dates.month(Settle) # compute month difference
years = Dates.year(Maturity) - Dates.year(Settle)
days = (years*12+months)*30
T = days/360
DataFrame(Call = Black.(AssetPrice,Strike,T,T̃,Rates,Sigma)[1][1], 
          Put = Black.(AssetPrice,Strike,T,T̃,Rates,Sigma)[2][2])

$Matlab \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; Julia$

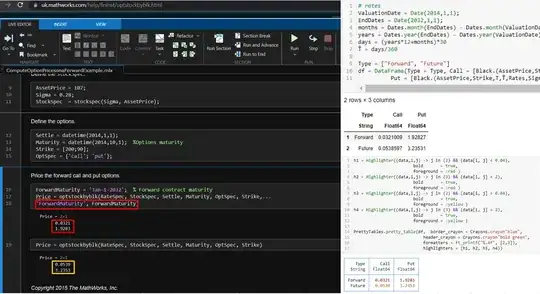
A bit more interesting is to check what happens when the expiry of the forward is set to a date far out. Within Matlab, if ForwardMaturity is not passed, the function calculates prices of future options. If ForwardMaturity is passed, the function computes prices of forward options. For the same option, setting ForwardMaturity to 'Jan-1-2032' (you can try this out yourself on Matlab's website) will give the following results (note, that the second result is an option on a future (or where the forward expires at option expiry).

$Matlab \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; Julia$

Call option on forward

1 Answers1