Black-Scholes volatility is average of local volatilities.
It is from: https://bookdown.org/maxime_debellefroid/MyBook/all-about-volatility.html
First what's the meaning of the average of all the paths between spot and the maturity and strike of the option? Here does path mean the underlying path satisfying
$$S_0=\text{Spot}\rightarrow S_T=\text{Strike}?$$
and does average means for each time $T',$ the BS implied vol
$$\sigma_{BS}(T',K) = average\Big[\sigma_{local}(S_i(T'))|S_i(0)=\text{Spot},S_i(T)=K\Big]?$$
here $i$ is the index of i-th path.
And I saw the similar result that local vol is the average of forward instantaneous vol:
$$\sigma^2(K,T)=E[\sigma^2_T|S_T=K],$$
do they say the same thing?
Also how to understand ATM volatility is the same for both Black-Scholes and Local Volatility?
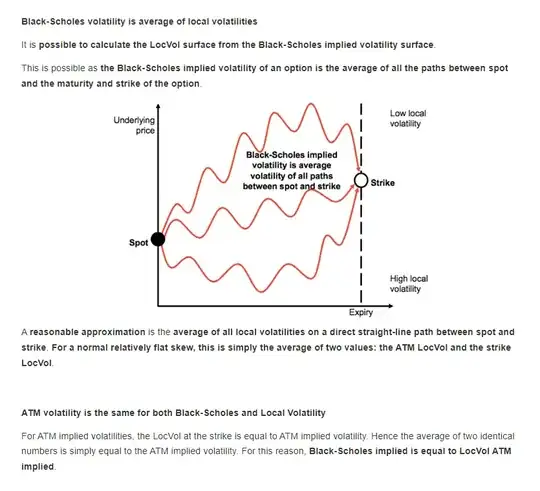

high local volatility). Seems it is the path of underlying price what I said above – user6703592 Nov 20 '22 at 17:19