5

I used Dupire's equation to calculate the local volatility as in https://www.frouah.com/finance%20notes/Dupire%20Local%20Volatility.pdf and Numerical example of how to calculate local vol surface from IV surface.

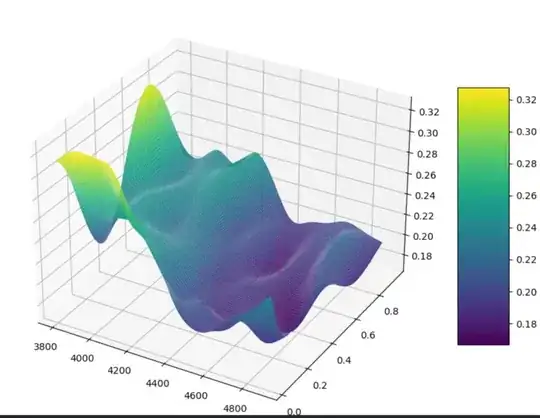
But my local volatility is very close to the smoothed implied volatility. (See the attached figure.). Shouldn't the lv line be more sharp (less smooth) than the iv line?

Volatility smile at one maturity

And I find that if I decrease the delta to 1e-4, the local volatility change sharply and becomes non-smooth. As the figure below: So is it right to set a very small strike delta when calculating its partial dirivative?

enter image description here

The code I used is below (the excel file is can be got from https://1drv.ms/x/s!AhPTUXN0QjiSgrZeThcRtn2lJJf6dw?e=t3xqt4):

import pandas as pd
import numpy as np
from scipy.stats import norm

Clean data


smooth_data = pd.read_excel('smooth.xlsx', converters={'TradingDate': str, 'ExerciseDate': str})
smooth_data.dropna(subset=['SoothIV'], inplace=True)
smooth_data = smooth_data[['Symbol', 'TradingDate', 'ExerciseDate', 'CallOrPut', 'StrikePrice', 
    'ClosePrice', 'UnderlyingScrtClose', 'RemainingTerm', 'RisklessRate', 
    'HistoricalVolatility', 'ImpliedVolatility', 'TheoreticalPrice', 'DividendYeild', 'SoothIV']]
smooth_data['RisklessRate'] = smooth_data['RisklessRate']/100


BSM formula


def bsm_price(t, S, K, r, q, sigma, OptionType):
    r = np.log(r + 1)
    q = np.log(q + 1)
    d1 = (np.log(S/K) + t(r - q + 0.5sigmasigma)) / (sigmanp.sqrt(t))
    d2 = d1 - sigmanp.sqrt(t)
    if OptionType == 'C':
        v = S(np.e(-qt))norm.cdf(d1) - K*(np.e(-rt))norm.cdf(d2)
    elif OptionType == 'P':
        v = K(np.e(-rt))norm.cdf(-d2) - S(np.e*(-qt))*norm.cdf(-d1)
    return v


Dupire formula


def local_vol(t, S, K, r, q, sigma, OptionType, deltat, delta):
    dc_by_dt = (bsm_price(t+deltat, S, K, r, q, sigma, OptionType) - 
                bsm_price(t-deltat, S, K, r, q, sigma, OptionType)) / (2deltat)
    dc_by_dk = (bsm_price(t, S, K+delta, r, q, sigma, OptionType) - 
                bsm_price(t, S, K-delta, r, q, sigma, OptionType)) / (2delta)
    dc2_by_dk2 = (bsm_price(t, S, K-delta, r, q, sigma, OptionType) - 
                2bsm_price(t, S, K, r, q, sigma, OptionType) + 
                  bsm_price(t, S, K+delta, r, q, sigma, OptionType)) / (deltadelta)
    sigma_local = np.sqrt((dc_by_dt + (r-q)Kdc_by_dk + (r-q)bsm_price(t, S, K, r, q, sigma, OptionType))/(0.5(KK)dc2_by_dk2))
    return sigma_local


Calculate local volatility


smooth_data['LocalVolatility'] = smooth_data.apply(lambda x: local_vol(x['RemainingTerm'], x['UnderlyingScrtClose'], 
    x['StrikePrice'], x['RisklessRate'], x['DividendYeild'], x['SoothIV'], x['CallOrPut'], 0.01, 1.5), axis=1)
nickzhy
  • 61
  • 3
  • Are you sure your data makes sense? You have a risk-free rate set to be 1.5, i.e., 100.5%, but a dividend yield of 0.009. Does that make sense to you? The strikes are in the region of 3400 to 5600, but the underlying asset prices are in the region of 0.4 to 368. I've never seen option prices with those characteristics, the market data looks completely odd. – AXH Aug 10 '22 at 00:43
  • Hi, AXH, you may misunderstood the data. In the data clean process, the risk free rate is divided by 100, so it is 0.015 actually. The "underlying asset prices" you mention is the close price of the option rather than the close price of the underlying asset. The close price of the underlying asset price is 4489.538, which is also a constant. – nickzhy Aug 11 '22 at 06:28

0 Answers0