0

If I measure daily returns by simple percent change, a -50% day then a +50% day (or vice versa) results in a true -25% total change, but the average makes it look like you would expect a total 0% change.

Is there a way to measure returns differently that eliminates this effect? For context I have two series of returns and the one with a lower average daily return ends up with a higher total return and I suspect this phenomenon is to blame.

Currently I measure daily return by: (priceDay2-priceDay1)/priceDay1

user708873
  • 11
  • 2

2 Answers2

8

Take the log return between days.

Newquant
  • 779
  • 1
  • 4
7

What does not work with the geometric mean?

The geometric mean is computed with the following formula: $${\displaystyle \left(\prod _{i=1}^{n}x_{i}\right)^{\frac {1}{n}}={\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}}$$

which is equivalent to the arithmetic mean in logscale (see Wikipedia):

$${\displaystyle \exp {\left({{\frac {1}{n}}\sum \limits _{i=1}^{n}\ln x_{i}}\right)}}$$

A quick implementation in Julia looks like this.

geom = ((1-0.5)*(1+0.5))^(1/2)-1
100*(1+geom)^2
(1+geom)^2-1
exp(1/2*(log(0.5)+log(1.5)))-1

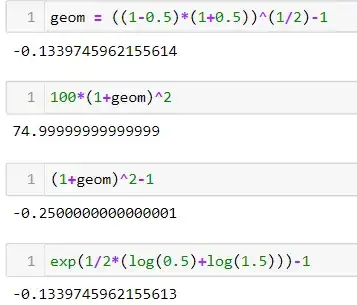
enter image description here

The inaccuracy is due to decimal precision of floating point math, see for example this answer.

While I think taking logs is generally useful, I do not really think using log returns is particularly meaningful (easy to interpret) in this example. While it is true that the sum of log returns in each period corresponds to the log return over the entire period, I am not sure what you can do with this result, unless you transform it back into the geometric mean as shown above.

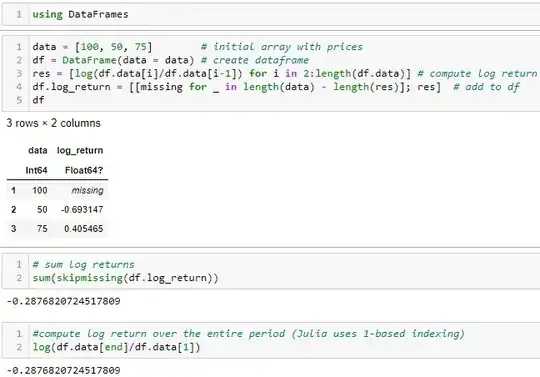
If you simply use the log returns, you get the following values: enter image description here

However, as you wrote, the true change is $-25\%$ and not $\approx -28.76\%$. Also, each period change ($-69.31\%$ and $+40.54\%$) is far from the actual change of $\pm 50\%$.

On the other hand, the geometric mean provides you with the constant growth rate (return) that yields the correct final amount.

AKdemy
  • 9,269
  • 1
  • 23
  • 90
  • Thanks for the detailed overview. What I meant by it doesn't work is that the geometric mean of returns gave a smaller value for the portfolio with higher total returns, which seems wrong to me. Maybe it's an implementation error on my side so I'll go through it again and post the code soon. – user708873 Jun 18 '22 at 22:18
  • 1
    Just went through my code and cleaned it up. I'm not sure what the issue was, but the geometric mean is now giving good results. Thank you – user708873 Jun 18 '22 at 22:48