In the book Derivatives Markets (McDonald, 3rd edition), there's a chapter on Monte Carlo valuation of option prices. It starts with simulating stock prices (p578) with the following equation:
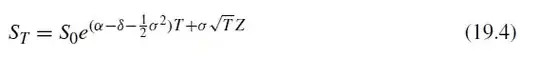
St = price after time T
So = starting price
alpha = risk-free rate
delta = dividend yield
sigma = volatility
Z = random variable drawn from standard normal distribution
To simplify things lets say that T = 1, alpha and delta = 0. But I also add in an expected underlying return variable, u. That would give the simulated stock price at end of period T to be:
St = S0^(u - 0.5 * sigma^2) + sigma * Z)
If I do 10000 simulations with the above equation, using S0 = 100, u = 0.03, sigma = 0.1, I get a mean St of 103.10.
If strike price (K) for a call was 100, I get a mean max[0, St - K] of 5.79. I interpret this as the fair price of the option.
If I instead set u = 0, I get mean St of 100.13 and mean max[0, K - 100] of 4.12.
According to this, the price of the option is depending on the expected return, u, of the underlying. But I've read 1000 times that the option price does not depend on expected return. Can someone clarify what I'm doing wrong?