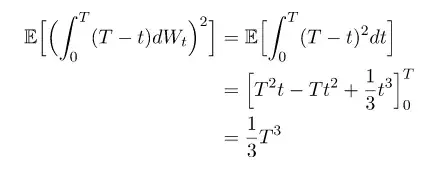Integration over function of Wiener process

Question

I wish to calculate below 3 expectations of a typical Wiener process -

1. $E \left[ \int\limits_{0}^{T} tdW_t \right]$
2. $E \left[ \left( \int\limits_{0}^{T} tdW_t \right)^2 \right]$
3. $E \left[W_T \int\limits_{0}^{T} tdW_t \right]$

How should approach them?

Answer 1

• Question 1) The Itô integral of a deterministic function is Gaussian, see here or here, i.e. $$\int_0^T f(u)\mathrm{d}W_u \sim N\left( 0,\int_0^T f(u)^2\mathrm{d}u\right).$$ The answer is thus zero. We of course need to require that $\int_0^T f(u)^2\mathrm{d}u<\infty$.

• Question 2) The simple version of Itô's isometry reads as $$\mathbb{E}\left[\left(\int_0^T X_u\mathrm{d}W_u\right)^2\right]=\mathbb{E}\left[\int_0^TX_u^2\mathrm{d}u\right].$$ Setting $X_u=u$, the answer is to question two is thus $\int_0^T u^2\mathrm{d}u=\frac{1}{3}T^3$.

• Question 3) Itô's isometry generalises to $$\mathbb{E}\left[\left(\int_0^T X_u\mathrm{d}W_u\right)\left(\int_0^T Y_u\mathrm{d}W_u\right)\right]=\mathbb{E}\left[\int_0^TX_uY_u\mathrm{d}u\right].$$ Thus,

$$\mathbb{E}\left[W_T\int_0^T u\mathrm{d}W_u\right]=\mathbb{E}\left[\left(\int_0^T 1\mathrm{d}W_u\right)\left(\int_0^T u\mathrm{d}W_u\right)\right]=\mathbb{E}\left[\int_0^T u\mathrm{d}u\right]=\frac{1}{2}T^2.$$

(Note: There is a typo in your question, the first Brownian motion should be $W_T$ and not $W_t$.)

Answer 2

For this type of problem you need to use the Ito isometry

1. The first one is 0 due to symmetry of $W_t$ around 0

2. A really similar problem is solved with working in this post (I've copied the algebra below): http://www.quantopia.net/interview-questions-vii-integrated-brownian-motion/

3. Looks like stochastic integration by parts might help here (also used in the post above)