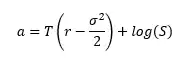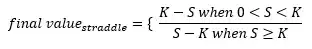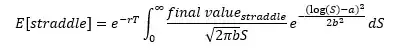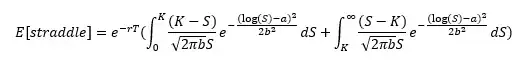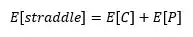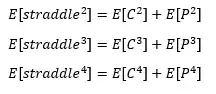Following the logic of Ben-Meir and Schiff (2012) and this question the first, second, third and fourth raw moments of a put are:
Similarity, for a call it is as follows:
where
and
S = spot price, K = strike price, r = risk-free rate, T = time to maturity and sigma is implied volatility.
I want to know what the third and fourth raw moments of a straddle are. A straddle consist of a call and a put
If S > K at maturity. then the call option will have a value of S - K, and the put will have no value.
Likewise if S < K, the call option will have no value, and the put will be worth S - K. This can be written as:
As a result the expected final value is equal to:
This can also be written as:
Which can be simplified to:
Following this logic for the other moments I get:
According to the theory about cumulants if two variables are independent, the n-th-order cumulant of their sum is equal to the sum of their n-th-order cumulants. Inspecting the final raw moments of the straddle it looks like this applies. However, a call and a put are not independent. When the value of a call increases/decreases, the value of a put decreases/increases, so the two option types are negatively correlated. This "fact" and the final results make me feel like I used the wrong assumptions.
Question: Are the the defined raw moments for a straddle correct or am I missing something?