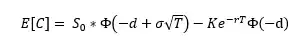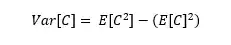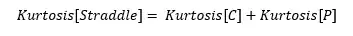I want to determine the kurtosis of a straddle. My question is closely related with the following topic here. According to the following paper of Ben-Meir and Schiff (2012) the expected value of a call is equal to
where
The variance of the call is
Following the standard definition of kurtosis I can write:
Similar, I can write the same for the puts:
Is it correct to assume that: