I have a hard time understanding how high IV effects the amount of gamma obtained via a put backspread. Is it via the angle on the payoff or via the ratio one gets i.e number of OTMs one can buy? or simply just that one has bigger numbers in the credit and debit for the position?
2 Answers
In a put back-spread, you are short one put and long two puts with a lower strike.
As far as Vega (the spread's price sensitivity to IV) is concerned, it depends on where you enter the spread. Usually, you'd enter the spread where the short put is at the money or near being at the money: this ATM put will have a high Vega, whist the two puts with lower strike will have a low vega to start with. So if the underlying price stays where it is, you're actually short Vega and increasing IV should increase the value of the short put more than the value of the two OTM puts. So in this scenario, increasing IV will lower the price of the spread.
As the underlying price moves lower and your short put becomes ITM, your two long puts will gradually come closer to being ATM. Since Vega is highest for ATM options, there will come a point where Vega on the two long puts will become higher than the Vega on the short put: then, increasing IV will increase the price of the spread.
Edit: picture below shows that deep OTM or ITM options have low sensitivity to IV (so if the options are on the SPX, the sensi to VIX for ITM or OTM options is much lower than for ATM options: that should answer your question as to "why the one ATM put benefits from higher VIX more than two OTM puts"):
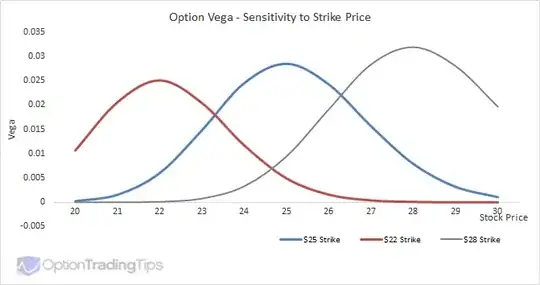
- 6,118
- 2
- 17
- 59
-
sorry this is not what I ment, I ment in terms when you put it on not how the price develops. In other words what difference does a high reading on the VIX make when you put on or buy a back spread in contrast to a low reading on the VIX. Dont erase the answer tho, the above was also nice to read. – user123124 Jun 22 '20 at 18:02
-
1So if you put on a back-spread on the SPX 500 then the VIX reading will directly affect the price of your spread in line with what I wrote. Imagine you enter the spread where the first option is ATM and the two lower-strike options are OTM. Then, higher VIX decreases the value of your spread, whilst lower VIX increases the value of your spread. If the SPX tanks though and the lower-strike options get closer to being ATM, then the relationship will change: higher VIX will increase the price of your spread and lower VIX will decrease it. The key concept is that your Vega changes with SPX price. – Jan Stuller Jun 22 '20 at 18:10
-
wouldnt a high VIX, which as far as I understand increase option prices, force on to go further OTM to get the two options matching up in price to the ATM? Since they are two and the other one is just "1". Its not the Vega but the amount of gamma I get that I am intrested in. – user123124 Jun 23 '20 at 05:27
-
Gamma is second order sensitivity to the underlying price. So if the options are on the SPX 500, Gamma would be the second order sensitivity to SPX price, NOT the VIX. Your only sensitivity to VIX is Vega (and Vomma, but let's not worry about Vomma for now). The two OTM options don't increase in price much when VIX goes up, because their Vega is very low, compared to the one ATM options. I added a picture to my answer that might help understand this graphically. – Jan Stuller Jun 23 '20 at 06:41
-
and so you are saying with a higher VIX I should be able to put on a 3:1 ratio instead of a 2:1 all else being equal? anyway, high iv should also affect gamma right i.e it flattens it. – user123124 Jun 23 '20 at 07:23
-
Let's say we're on the graph above in my answer: the underlying price of the SPX is 25 (as an example), and your ATM put's Vega corresponds to the blue function. Your two OTM puts have Vega that correspond to the red function. The red Vega at spot 25 is about 0.005, whilst the blue vega at spot 25 is about 0.03. So the blue Vega is about 6-times higher: therefore when VIX goes up, your ATM put will increase in price six-times as much as one of your OTM puts. Ps: yes, Gamma is also affected by IV. But Gamma will only manifest itself once the underlying spot starts moving. – Jan Stuller Jun 23 '20 at 07:30
-
I think we misunderstand each other..you seem to describe how changes in IV effects the value of the position, looking back at my question I can see how one would think that this is what I am asking. Sorry about that. I should been more explicit, what I want to know is how an high IV environment(like now 30+) effetct the amout of gamma one obtains via this spread. The purpose of opening it is going long vol. – user123124 Jun 23 '20 at 07:38
-
I suppose I want sell a small amout of gamma and buy a lot of gamma to be long gamma. And so I want low vol for the gamma to be low for the ATM and high vol to have high amout of gamma on the OTMs. Which is sort of incomparable..my intuition tells me this cancels out since I am on both sides when doing this trade in some sense. But I am not sure, since there is a trade off in the sense that you can compensate buy going further out OTM. Less OTM means less vol required to start profiting. How IV effets the postion is intersting as well tho in it own right, so the missunderstading was OK :D – user123124 Jun 23 '20 at 07:45
-
https://youtu.be/pvX5_rkm5x0?t=1736, he claims low vol gives you more gamma. copied at the right time of the statement. – user123124 Jun 23 '20 at 07:49
-
another comment https://youtu.be/pvX5_rkm5x0?t=2041 – user123124 Jun 23 '20 at 07:56
-
Gamma is highest for ATM options, so again, your Gamma would be higher for your ATM put than it would be for our two OTM puts. So you would be short Gamma to start with on your spread. Effect of IV on Gamma is quite an advanced topic: increasing IV will lower gamma. So what might happen is that: (i) you enter the spread & you're initially short Gamma (because your ATM put has higher gamma than your OTM puts). Then as IV increases, the Gamma of all your puts decreases, but it will decrease more on your ATM put. So you might eventually end up being long Gamma if IV increases substantially. – Jan Stuller Jun 23 '20 at 09:22
-
exellent point. isnt the gamma of a postion the sum of the gammas? and so when you go ratio then one can add OTMs to surpass the ATM that you sell. – user123124 Jun 23 '20 at 09:29
-
Yes: depends on how deep OTM the two OTMs are. The gamma graphs look very similar to the Vega graphs I posted: so the maths works the same way. If your OTM puts are very deep OTM, you'd need to buy more than just two of them to overpower the short gamma on the ATM put. If the strikes are relatively close to each other and the OTM puts are not deep OTM, then two OTM puts might be enough to be net long gamma. – Jan Stuller Jun 23 '20 at 09:32
-
high IV is not that easy to consider then..if you have high IV i.e flat gamma curve then it should be easier to over power the gamma? Which would make it more favorable in contrast the youtube statements. Also my conclusion is then that you wanna get high gamma per dollar on your long OTMs in the end, but high IV gives higher prices.. – user123124 Jun 23 '20 at 09:44
-
Agreed that if you wanna be long gamma overall you wanna get high gamma per dollar on your OTM puts. Computing gamma is not difficult, the formula is simple. You've got a good maths background (judging by your reputation on maths stack exchange :): I've found it helpful to do a simple investigation in Excel: the three puts will be identical except for IV and strikes. The spread gamma is the sum of individual gammas: just experiment a bit with the strikes and IV in excel and you'll quickly see where the break-even points lie. – Jan Stuller Jun 23 '20 at 09:56
-
Thanks for the input and feedback! – user123124 Jun 23 '20 at 10:04
-
Is increasing IV really lowering gamma for OTM options? – user123124 Jun 25 '20 at 17:22
-
@user1: I answered below. – Jan Stuller Jun 25 '20 at 17:45
Below, Gamma is denoted by $\Gamma$, and $IV=\sigma$:
$$ \Gamma = \left(\frac{1}{S_0*\sigma*\sqrt{T}}\right)*\left(\frac{1}{\sqrt{2\pi}}e^{\frac{-d_1^2}{2}} \right) $$
The expression in the first bracket is inversely proportional to $\sigma$, so isolating just this first expression: higher $\sigma$ will trivially lower this first expression.
The second bracketed expression is a Standard Normal PDF, where:
$$d_1=\frac{ln\left(\frac{S_0}{Ke^{-rT}}\right)}{\sigma\sqrt{T}}+0.5\sigma\sqrt{T}$$.
For OTM put options, $ln \left( \frac{S_0}{Ke^{-rT}} \right)$ is positive, because $S_0>Ke^{-rT}$. So increaing $\sigma$ will make this log-term smaller, which will make $d_1$ closer to zero and therefore the PDF $\left(\frac{1}{\sqrt{2\pi}}e^{\frac{-d_1^2}{2}} \right)$ will move closer to its peak. At the same time, increasing $\sigma$ will make the expresison $0.5\sigma\sqrt{T}$ larger, moving the $d_1$ away from zero, and therefore moving the PDF away from its peak.
So in conclusion: increasing IV decreases the first bracketed expression, and it is not possible to say with certainty whether it increases or decreases the second bracketed expression: whether the second bracketed expression increases with increasing $\sigma$ will depend on:
(i) how much OTM the option is,
(ii) the current level of $\sigma$,
(iii) Time to maturity $T$.
In general, increasing IV decreases Gamma via the first bracketed expression, but there can be limited cases where deep OTM options will gain Gamma from rapid increases in IV. To get a clearer idea, the best way to go about this is to try to plot the gamma for different strikes and play around with the $\sigma$ parameter.
- 6,118
- 2
- 17
- 59
-
Thanks, I did some calculations on 10 % OTM montly puts and gamma inceased going from vol 25 to 30. Dunno weather that is considered far OTM, I am not really a experienced options trader. – user123124 Jun 25 '20 at 18:30