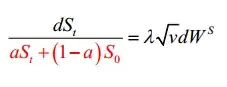If we take the heston model but change it slightly by introducing a new parameter $\alpha$ such that
is there a way to price the call option within this model as, maybe, a function of the call price within the original model? Or a function of $S_T$ as simulated from the original model?
Let $X_t = a S_t+(1-a)S_0$. Then \begin{align*} dX_t &= adS_t=a\lambda X_t \sqrt{v_t} dW^S_t,\\ X_0 &= S_0. \end{align*} Moreover, \begin{align*} \max(S_T-K, 0) &= \max\left(\frac{1}{a}X_T - \frac{1-a}{a}S_0 -K, \, 0 \right)\\ &= \frac{1}{a}\max\Big(X_T-\big(aK-aS_0+S_0\big), \, 0 \Big). \end{align*} You can now value the option using the previous formula or Monte Carlo approach, assuming that the underlying asset process is represented by $\{X_t, \, t \ge 0\}$.
if we change coordinates slightly, we can regard the process as $$ d (S+\alpha) = (S+\alpha) r dt + \lambda(S+\alpha)\sqrt{V} dW_t, $$ so it's an option on $S+\alpha$ with $S+\alpha$ following the Heston process. So just take the old formula and add $\alpha$ to spot and strike.
