15

I have already figured out that Delta-hedging essentially turns European options into volatility products where you pay implied vol and get paid realized vol for long positions and you pay realized vol and get paid implied vol for short positions. I have also discovered that market-making in European options generally is conducted by using volatility models to project vol for some underlying asset and then quoting bid and ask prices using the pricing model subject to the projected vol and finally delta-hedging all option positions that get filled by the market.

What is the effect of delta-hedging exotic options? Does it have the same effect of turning the exotic options into volatility-based payoff products as opposed to directional price movement payoff products? Do market-makers in exotic options delta-hedge their positions just like is done with vanilla products?

Alex Ockenden
  • 327
  • 2
  • 10
  • I am sure they attempt to hedge then in some manner, but it is much harder to do and I suspect the hedging is less effective, i.e. more idiosyncratic risk is passed through. The general concept is the same. – Alex C Oct 02 '16 at 15:21
  • 2
    Yeah generally I'm sure you're right, but what is the POINT of hedging exotic options? With vanilla options the point of delta hedging is to profit from volatility not directional price movements. The same does not seem to apply to exotic options. I am just running some Matlab simulations and I see that when delta-hedging a binary option, profit is apparently NOT strongly correlated to realized vol. In fact, I see no discernible relationship between realized vol and profit at all. – Alex Ockenden Oct 02 '16 at 22:15
  • @AlexOckenden what do you mean by pricing model? – Trajan May 30 '18 at 21:24

2 Answers2

23

Consider reading Lorenzo Bergomi's excellent book -- or at least the first chapter available here for download --, it will help you clarify things.

Some remarks as to your original question:

  • It is well known that, under a pure diffusion assumption, the total P&L of a delta hedged European option (i.e. an option whose payoff only depends on the value of the underlying asset at a future date $T$) over the horizon $[0,T]$ writes: $$ P\&L_{[0,T]} = \int_0^T \frac{1}{2} \underbrace{\Gamma(t,S_t,\sigma^2_{t,\text{impl.}})S_t^2}_{\text{Gamma dollar}}( \sigma^2_{t,\text{real.}} - \sigma^2_{t,\text{impl.}}) dt $$ As such, although a delta hedged European option portfolio is sensitive to the realised vs. implied volatility discrepancy, it is not a pure volatility trade: the Gamma dollar term introduces a dependency on the spot path. This Gamma dollar term should really be seen as some kind of volatility accumulator: only along paths where the Gamma dollar is non zero will the discrepancy between realised and implied volatility matter.
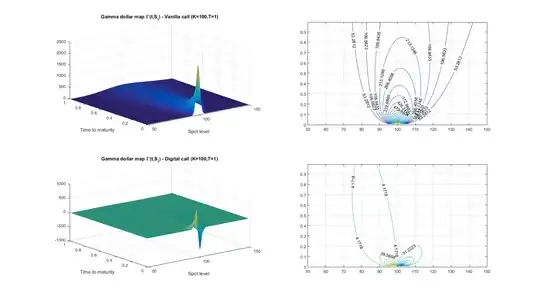
  • The previous relationship still holds for digital (or binary) options, since they are also European options after all. What you observe is thus simply a consequence of the fact that the Gamma map of a binary call is pretty different from that of a vanilla call (see below): indeed, it is zero over most of the time to maturity/spot domain. As such the contribution of realised vs. implied volatility discrepancies to the total P&L is completely different: only what happens (1) around the strike, (2) near the expiry matters. This is why you did not observe a strong correlation between the resulting P&L and the realised vol over the entire delta-hedging horizon.

enter image description here

Now with respect to delta hedging exotic options, quoting from Lorenzo Bergomi's "chapter's digest" and adding some of my own remarks:

Delta hedging removes the order-one contribution of $\delta S$ to the P&L of an option position.

Although the expectation of the P&L of a delta hedged portfolio is zero (provided you correctly anticipate the volatility - or variance - of future returns),

Delta hedging is not adequate for reducing the standard deviation of the P&L [...] The sources of the dispersion of this P&L are: (a) the tails of returns, (b) the volatility of realized volatility and the correlation of future realized volatilities.

Using options for gamma-hedging (...)

In other words, using other vanilla options to locally cancel the gamma dollar term,

immunizes us against realized volatility (...) Dynamical trading of vanilla options, however, exposes us to uncertainty as to future levels of implied volatilities.

Hence the need of stochastic volatility models for modelling the dynamics of implied volatility.

Exotic options often depend in a complex way on the dynamics of implied volatilities

An exposure which is usually dealt with by trading vanilla options. See for instance the case of a (relative) forward-start at the money call in a homogeneous diffusion model. In that very specific case, we do not care about delta hedging anymore since it is only the dynamics of forward volatility that matters. One way want to neutralise such an exposure using calendar spreads.

Community
  • 1
Quantuple
  • 14,622
  • 1
  • 33
  • 69
  • 1
    +1 for recommending Bergomi's book - one of the most useful/practical ones I own. – LocalVolatility Oct 04 '16 at 12:48
  • @LocalVolatility, it is indeed a very nice piece of work. – Quantuple Oct 04 '16 at 12:52
  • 1
    Interesting remark about Binary Options, had not fully realized until today "dollar gamma vol integral" has implications for them also. – nbbo2 Oct 04 '16 at 13:05
  • 1
    @noob2 glad I raised an interesting point. Sometimes it is indeed easy to forget that binary options are merely call/put spreads and not that exotic as such (although pretty exotic to hedge in practice). – Quantuple Oct 04 '16 at 13:12
  • 2
    Wonderful answer. I'd upvote again if I could. – experquisite Oct 04 '16 at 18:23
  • Yes, no gamma = no convexity, i.e. your option position is basically equivalent to a position in the underlying itself (since it's value is strictly linear in $S$). As such, volatility has no role to play: the option position and the stock position already perfectly compensate each other as the underlying moves, there is no P&L (at least over an infinitesimally small period of time). For volatility moves to matter, you need convexity, see the notion of "break-even volatility". Have you read Chapter 1 of the book ? – Quantuple Oct 05 '16 at 14:12
  • Thanks for the in-depth answer. Your gamma map shows that delta does not change by any appreciable amount when the current underlying price is away from the strike, and when there is significant time remaining to maturity, correct? This means that the delta-position does not take full advantage of movements in price for most of the life of the option, and therefore does not add to P&L?

    I plotted terminal prices vs profits: http://imgur.com/a/WJhzC

    Is this relationship due to the high sensitivity of delta near the strike and when close to expiration?

    I will read the chapter today.

     – Alex Ockenden Oct 05 '16 at 14:12
  • Well look at the pattern you get, looks similar to the gamma map at $t=T$ no ? By plotting $P&L_{[0,T]}$ versus $S_T$ you are using the hidden relationship $P&L_{[0,T]}$ is approximately equal to the Gamma dollar close to expiry times the vol discrepancies, where the Gamma dollar is itself a function of $S_T$. Informally: $P&L_{[0,T]} \approx P&L_{[T-\Delta t, T]} = \frac{1}{2} \Gamma(T-\Delta t ,S_{T-\Delta t}) S_{T-\Delta t}^2 (\sigma^2_{r. [T-\Delta t, T]}-\sigma^2) \Delta t = f(S_{T-\Delta t}) \approx f(S_T) $. – Quantuple Oct 05 '16 at 14:21
3

Delta-hedging can be seen from banks as "manufacturing the product". Banks are product manufacturers, so they delta-hedge.

Exotic options are options which are not volatility-only products. They depend on volatility dynamics. Delta-hedging exotic options need most of the time to use vanilla options in the hedging portfolio.

M. Jeunesse
  • 2,422
  • 10
  • 20