In Shreve's book, future process is defined to be a stochastic process that satisfies the following two conditions:
(1) $Fut_s(T,T) = S(T)$ where $Fut_s(T,T)$ is the future price at expiration and S(T) is the price of the underlying.
(2) At any time $t_k$, the value of the (daily settlement) payment to be received at time $t_{k+1}$ and indeed all future times is zero.
As a consequence of the second condition, the book claims that the future price process has to follow the following equation:
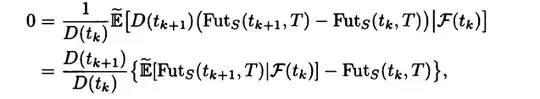
I understand that the expectation of the right hand side should be zero by condition (2). Can anyone explain why is it not zero under the true probability measure instead of the risk neutral measure?
Note: This is question is from page 243 of Shreve's Stochastic Calculus for Finance