The value of European binary call, paying \$1 if $S_T > K$ or nothing otherwise, is
$$c_t=e^{-r(T-t)}N(d_2)$$
where, $d_2=\frac{ln(S_t/K)+(r-\sigma^2/2)(T-t)}{\sigma \sqrt{T-t}}$
Delta of your binary call option is $$\Delta_t=\frac{\partial c_t}{\partial S_t}=\frac{e^{-r(T-t)}N'(d_2)}{\sigma S_t \sqrt{T-t}}$$
Derivation
We need to compute
$$\Delta_t=\frac{\partial c_t}{\partial S_t}$$
$$\frac{\partial c_t}{\partial S_t}=\frac{\partial}{\partial S_t}\bigg(e^{-r(T-t)}N(d_2)\bigg)=e^{-r(T-t)}\frac{\partial}{\partial S_t}N(d_2)$$
$$\frac{\partial}{\partial S_t}N(d_2)=\frac{\partial}{\partial S_t} \int_{-\infty}^{d_2} \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2}dx$$
where $d_2=f(S_t)$. Using Leibniz integral rule
$$ \frac{\mathrm{d}}{\mathrm{d}x} \left (\int_{a(x)}^{b(x)}f(x,t)\,\mathrm{d}t \right) = f(x,b(x))\cdot b'(x) - f(x,a(x))\cdot a'(x) + \int_{a(x)}^{b(x)} \frac{\partial}{\partial x}f(x,t)\; \mathrm{d}t. $$
So, $$\frac{\partial}{\partial S_t} \int_{-\infty}^{d_2} \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2}dx=\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}d_2^2} \frac{\partial}{\partial S_t} (d_2)$$
You may check it yourself that $$\frac{\partial d_2}{\partial S_t}=\frac{1}{S_t \sigma \sqrt{T-t}}$$
Putting all the results together
$$\frac{\partial c_t}{\partial S_t}=\frac{e^{-r(T-t)}N'(d_2)}{\sigma S_t \sqrt{T-t}}$$
where $N'(d_2)$ denote the standard normal probability density function,
Relationship between Binary option delta and Time to expiry
@dm63 already provided a brief answer to your question how delta will respond as option will approach its expiry, below I have shown more accurate relationship
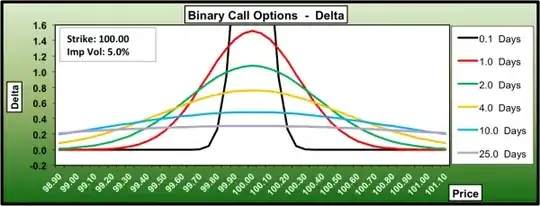
Ref: http://www.binaryoptions.com/binary-option-greeks/binary-call-option-delta
You can see as the time to expiry decrease the delta of an at-the-money option approaches to infinity. Because a small change in stock price ($\epsilon$), assume $S_t=K$ and option is near maturity, will cause the option payoff to change its value by \$1 (as information provided in OP). So, option delta $\Delta_t= \frac{1}{\epsilon} \to \infty$. You may also check this result from formula derived above.
