I am investigating some asset allocation strategies and I am wondering about the results I obtain. I am working on monthly and weekly data of the same stock indices (SP500, FTSE 100 etc). And when I compute the summary statistics of the realized returns I observe that for the very same strategy those statistics vary greatly between weekly and monthly data. For the monthly f.e. I obtain skewness = 0.4 and kurtosis = 5, while for the weekly frequency skewness = 1.5 and kurtosis = 25.
Are the results for the weekly data plausible? And is it possible that the difference in the frequency of data results in such differences in the summary statistics? All computations are identical, the only difference is the data frequency.
I hope the question is not too general and it is possible to give some insight based on my description.
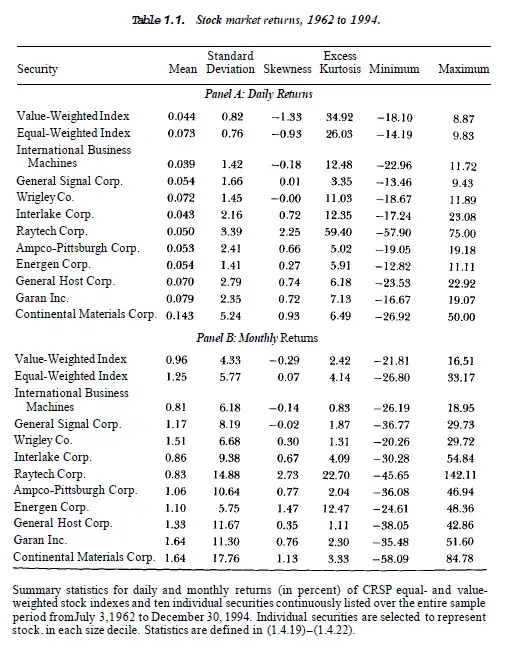
dodgyforvanillaindexes although some differences are expected but not thathuge(focusing on the kurtosis side). Please make me a favor by re-checking your weekly return series to see if there are no outliers, errors there. Alternatively specify your time horizon... As a matter of fact got6.559...(weekly) forspxfrom jan-99 til nov-15 vs10.63..(weekly)forukxfrom jan-98 til nov-15. hope you understand more about my reluctance here. Please quickly use Excelkurt()on your data and keep me posted as I am curious.– owner Dec 02 '15 at 22:03intra-daycalculations vsother frequenciesonfx markets, and am fine to discover something unexpecteda priorifrom yourasset allocationproblem. – owner Dec 02 '15 at 22:46Heavy Tails in High-Frequency Financial Data(Ulrich A. Muller, Michel M. Dacorogna && Olivier V. Pictet) from textbookA Practical Guide to Heavy Tails(Adler, Feldman && Taqqu). Interestingly they evidence that"for shortest time intervals (tick-by-tick data), estimates of kurtosis are clearly greater than 3 ([13:45]) but in general kurtosis decreases with increasing time intervals approaching towards gaussian values (at around 1 week)". I have to concede I can't generalize these findings to your strategic allocation problems but it's worth reading the paper. – owner Dec 03 '15 at 07:59