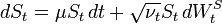
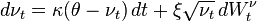
Why do we model it as sqrt root of v(t)? Is that because we don't want the volatility to go negative? If this is the case, can we model it as square of v(t)?
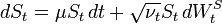
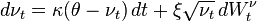
Why do we model it as sqrt root of v(t)? Is that because we don't want the volatility to go negative? If this is the case, can we model it as square of v(t)?
V(t) is the variance process of the stock price, not volatility process. Cox-Ingersoll-Ross demonstrated that that specific process can be non-negative under certain conditions, which is what you want for variance.
In this paper http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2626552 the authors compare the Heston model with volatility given by
$ dV_t = \kappa_V(\bar{V}-V_t)dt+\sigma_V\sqrt{V_t}dW_t $
with the a model where the volatiltiy is given by
$ dV_t = \kappa_V(\bar{V}-V_t)dt+\sigma_VV_tdW_t $.
They show that the latter is inverse gamma distributed and leads to a more stable volatility distribution with higher kurtosis and fater tails.
However, a quick read shows, that the inverse gamma model seems to be relatively unexplored.
The reason is that Heston managed to solve the case with square root. The log-normal vol process leads to nasty properties. The 3/2 model is another case that have been solved.
we assume $X_t$ follows the differential stochastic process $$d X(t)=\mu (t,{{X}_{t}})dt+\sigma (t,{{X}_{t}}) dW(t)$$ if $$\underset{{{X}_{t}}\to 0}{\mathop{\lim }}\,\,\mu (t,{{X}_{t}} )-\frac{1}{2}\frac{\partial }{\partial x}{{\sigma }^{2}}(t,{{X}_{t}})\geq 0$$ then $$P(\{\,t\in [0\,,\infty )|\,X(t\,,x )\leq 0\})=0$$
in the C.I.R Model ,we have $$\underset{{{v}_{t}}\to 0}{\mathop{\lim }}\,\,\left( \kappa (\theta -{{v}_{t}})-\frac{1}{2}\frac{\partial }{\partial v}{{(\sigma \sqrt{{{v}_{t}}})}^{2}} \right)=\underset{{{v}_{t}}\to 0}{\mathop{\lim }}\,\,\kappa (\theta -{{v}_{t}})-\frac{1}{2}{{\sigma }^{2}}=\kappa \theta -\frac{1}{2}{{\sigma }^{2}}$$ another property of the square-root process for instantaneous variance is the fact that it leads in many case of interest to close-form or semi-close form solution for the characteristic function. we are also able to drive a close-form solution based on hyper-geometric functions when the underlying follow as mean reverting process.