I have the following likelihood function:
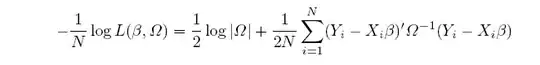
I'm given this information about the $\Omega$ matrix ($\boldsymbol{1}$ is a $T \times 1$ vector of ones):
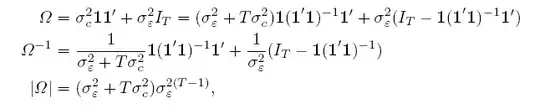
I would like to be able to show that the likelihood function can be rewritten to this:
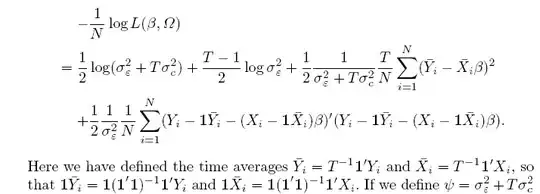
I think there is a misprint in the article, hence the screen images from the article I attached are wrong, meaning that $\Omega^{-1}$ is supposed to be $$\Omega^{-1}=\frac{1}{\sigma^2_{\varepsilon}+T\sigma^2_{c}}\boldsymbol{1}(\boldsymbol{1}'\boldsymbol{1})^{-1}\boldsymbol{1}'+\frac{1}{\sigma^2_{\varepsilon}}(I_t-\boldsymbol{1}(\boldsymbol{1}'\boldsymbol{1})^{-1}\boldsymbol{1}')$$
and not as stated above.
So far I've inserted the expression for $\Omega^{-1}$ in the top log-likelihood function. However, especially the last expression of the rewritten log-likelihood function bothers me, i.e. this part:
\begin{equation*} \begin{split} ...& &+\frac{1}{2}\frac{1}{\sigma^2_{\varepsilon}}\frac{1}{N}\sum_{i=1}^{N} \left(Y_i-\boldsymbol{1}\bar{Y}_i-\left(X_i-\boldsymbol{1}\bar{X}_i\right)\beta\right)'\left(Y_i-\boldsymbol{1}\bar{Y}_i-\left(X_i-\boldsymbol{1}\bar{X}_i\right)\beta\right). \end{split} \end{equation*}
Does anyone see the solution?
I also have this lemma, but not sure if it is to be used in the rewritting of the likelihood function:
