52

The lion plays a deadly game against a group of 100 zebras that takes place in the steppe (= an infinite plane). The lion starts in the origin with coordinates $(0,0)$, while the 100 zebras may arbitrarily pick their 100 starting positions. The the lion and the group of zebras move alternately:

  • In a lion move, the lion moves from its current position to a position at most 100 meters away.
  • In a zebra move, one of the 100 zebras moves from its current position to a position at most 100 meters away.
  • The lion wins the game as soon as he manages to catch one of the zebras.

Will the lion always win the game after a finite number of moves? Or is there a strategy for the zebras that helps them to survive forever?

Mike Earnest
  • 32,336
  • 6
  • 92
  • 237
Gamow
  • 45,573
  • 10
  • 147
  • 381
  • 7
    If zebras choose a place at an infinite distance,then lion can never catch them even if zebras arent allowed to move, for a simple reason that 100m covered by lion is a finite number & he needs to catch zebras in a finite no of moves, so the product of two finite numbers(100 & #no of moves) can never be infinite.So this would make the puzzle itself meaningless.So it must be mentioned that zebras can take position at a finite distance from lion only. – Sumedh Feb 16 '15 at 20:16
  • 8
    @Sumedh All positions on an infinite plane are at a finite distance from the origin. There is no need to mention that. – JiK Feb 17 '15 at 07:41
  • I think the above solutions ignore the fact that the zebra the lion is chasing chasing is not necessarily the one it will catch eventually. He needs to employ a strategy where he is approaching the majority of the Zebras at some stage. There are 99 zebras not moving. In the "solution" above the Lion would chase one zebra until above the rest and the majority were below and to the right (for example). Then come back down straight at the nearest zebra. The goal to force the nearest zebra towards other zebras. A soon as that zebra branched away the lion changes it attention to pushing another zeb –  Feb 17 '15 at 05:26
  • 2
    @JiK,yes you're right,but some of the answers given below consider initial distance between lion & zebras infinite.thats the reason the need arises to explicitly mention, as not everyone understands it implicitly. – Sumedh Feb 17 '15 at 12:13

4 Answers4

62

Zebras win.

Here is the strategy:

The zebras choose 100 vertical strips on the steppe, each of width 300m. The strips do not intersect. Each zebra promises to stay horizontally centered on its own individual strip.

 

If the lion enters a strip, then the zebra in that strip flees vertically away from the lion until the lion leaves the strip.

It works because:  

The lion cannot kill a zebra on the turn it moves into a strip, because the strips are too wide. And if it is already inside a strip, then the zebra in that strip has just moved 100m away from it, so it cannot catch the zebra.

Lopsy
  • 7,964
  • 30
  • 54
  • 1
    +1 Simple, beautiful, gives a concrete explicit strategy, and shows why it is correct. – JiK Feb 16 '15 at 15:14
  • 3
    I have a counterquestion. What if the lion's victory condition is not to catch a zebra, but instead to get within a leisurely 1mm of one? If no one sees an obvious answer to this, I'm going to post it as a separate puzzle. – Lopsy Feb 16 '15 at 15:48
  • 1
    Doesn't work for 1mm. The best approach you can make is 50/sqrt(2)m. – Joshua Feb 16 '15 at 16:35
  • 1
    What strip(s)? It is an infinite plane, which implies no 300 meter strips or canyons. Flees vertically? That sounds like they are helicopters, not zebras. – Michael Rize Feb 16 '15 at 16:56
  • @MichaelRize …what? – wchargin Feb 16 '15 at 17:02
  • This is not a good solution because the lion can move diagonally across the strips, and since all zebras are facing the same direction, they are easier to catch than if they are all facing different directions away from the lion. Also, there is no mention about the starting distance the zebras are from the lion. Very flawed. – Michael Rize Feb 16 '15 at 17:08
  • 1
    @MichaelRize The lion can move across the strips, but it is considered in the question. When a lion enters new strip, its distance to any lion is at least 50 m. The zebra will then jump away, creating a distance at least $\sqrt{50^2 + 100^2}$ m. – JiK Feb 16 '15 at 17:24
  • 1
    @MichaelRize When I said "vertically", I meant in the north/south direction, i.e. as if you were viewing the plane from above. I don't understand your second comment about the zebras facing different directions. – Lopsy Feb 16 '15 at 17:25
  • @MichaelRize For the completeness of the answer, it indeed could be explicitly mentioned that if the lion has the first move, any zebras will not start at distance less than 100 m from the lion. – JiK Feb 16 '15 at 17:26
  • 3
    @Joshua If the zebras adopt this strips strategy, then it is possible for the lion to get 1mm from a zebra. The lion enters a strip at the closest point to one of the zebras, and then chases the zebra vertically at a very very slight diagonal. – Lopsy Feb 16 '15 at 17:27
  • 4
    @MichaelRize To give an explicit example: The zebras number themselves $1,2,\dots,100$. The zebra $i$ starts at the position $(300i,0)$ (units are meters here and in what follows). When it is the zebras' turn, they will decide their move by the following algorithm: If the lion's $x$ coordinate is (strictly) larger than $300i-150$ and (strictly) smaller than $300i+150$ for an integer $i$ in $1,2,\cdots,100$, the $i$th zebra will move. Note that this cannot be true for two different values of $i$. (cont'd) – JiK Feb 16 '15 at 17:32
  • (cont'd) Now if the $y$-coordinate of the $i$th zebra is larger than the $y$-coordinate of the lion, the $i$th zebra will move 100 meters to the positive $y$ direction. Otherwise the $i$th zebra will move 100 meters to the negative $y$ direction. The subset of the plane where the $x$-coordinate is between $300i-150$ and $300i+150$ for some $i$ is called a strip in this answer. – JiK Feb 16 '15 at 17:33
  • Yes, but the lion is not limited to north/south directions. The lion can move in a somewhat diagonal direction across the various "strips". The lion's direction will take it closer to not only one zebra but multiple zebras. Since only one zebra can move at a time. Also the writer of the answer still has not specified the zebra's starting distance. If the zebras are less than 100 meters away, the lion wins, regardless of strategy. For this reason, I am surprised how many upvotes this got. – Michael Rize Feb 17 '15 at 05:01
  • 3
    @MichaelRize The fact that the lion can go across various strips is considered in the answer. The zebra in the current strip is always more than 100 meters away, and if the lion changes a strip, the zebra in the new strip will immediately jump so that it is more than 100 meters away. – JiK Feb 17 '15 at 06:54
  • 201m is apparently sufficient for a minimal distance between 2 zebras, since it suffice to prevent the condition of 2 zebras in the 100m radius at one point. – njzk2 Feb 17 '15 at 16:25
  • see the diagram on my answer, proving that this strategy is worse and actually makes it easier for the lion to catch a zebra. – Michael Rize Feb 20 '15 at 04:12
13

This is not an answer, but rather a counter to Micael Rize's answer. I don't intend for this to be picking on him, but it is too difficult to explain in a comment, and there are many arguments about his answer, so hopefully this will be persuasive.

In my example, I am going to use only 16 zebras, but it should be obvious that this is can extend to 100 zebras as well.

This is the starting configuration.

Initial configuration

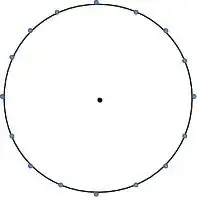
Now, lets say the lion chases the zebra to the east. After the first move, that zebra is the closest, so it will move directly away from the lion. Subsequent moves will bring the lion closer to the zebras adjacent to the zebra being chased, so they will have to move as well, always directly on a path from the origin according to the strategy. After a while (trillions of years), you will have the following setup.

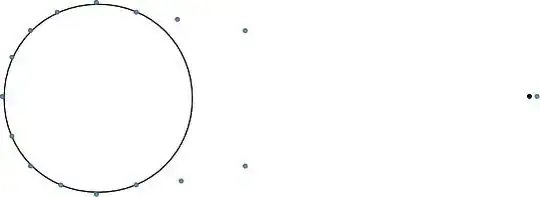
Chased away

Even though the lion looks close to the zebra, since the starting configuration was so immensely large, they are still light years apart and this zebra is in no danger of being eaten. The only reason the lion caught up is that the lion made many more moves than this zebra because the other zebras were forced to move at one point. Now, however, the zebra is able to move every time the lion moves, so can stay in front indefinitely.

In any event, this is where the lion changes tactics. Instead of chasing down the current zebra (pointless), he heads straight north. The zebra will continue to move outwards since it is still the closest. Eventually, you will get to the point where it is no longer the closest zebra, like so.

New Target

Now the lion turns back to the pack and chases the closest zebra in the circle (Red). According to the strategy, this zebra can only move outwards from the origin which gets closer to the lion obviously allowing the lion to capture it. The other option along this path is to move closer to the origin. While this is away from the lion, it will eventually meet and surpass the other zebra in red on the opposite side of the circle. Even if we ignore the fact that the other zebras will all move a bit as the lion runs through the centre of the circle, the lion is now chasing two zebras. According to the strategy, they can only move away from the origin, so they will always stay together. Thus, the lion is twice as fast as them and will catch one eventually.

There are probably different strategies that this zebra can take to avoid capture (e.g. taking different paths not directly from the origin), but the current answer is not sufficient to explain how to stay away from the lion.

Trenin
  • 8,964
  • 21
  • 53
3

Later: At the time, I was thinking of a solution similar to Lopsy's, but instead of vertical stripes I had an idea of circular sectors. Each zebra would thus have its own angle of 3,6°. Here is how I put it to words back then:

Zebras can win.

This is not a rigorous proof, but a good proof nonetheless.

The game is lost, if a lion can pick a new point $P$, such that at least two zebras are contained in a circle with a center at $P$ and radius of 100m. That is obvious, then only one zebra can escape in the next turn and at least one gets eaten.

So our objective is: after every zebra move, all zebras have to be more than 100m away from each other - this guarantees lion cannot make a move that would capture two zebras in the same 100m radius circle.

Since a zebra can move 100 meters, that just means it has to have some free space in some direction, e.g. it can move to a new point, not falling into 100m radius of another zebra.

This is easily achievable if we initially place zebras on the border of any convex shape, such as a circle of a square of an adequate size (adequate means each zebra is more than 50m apart).

Rok Kralj
  • 246
  • 1
  • 3
  • "all zebras have to be more than 50m away" Presumably you mean 200 m? – JiK Feb 16 '15 at 14:00
  • I guess that the lion can start chasing one zebra and get outside the convex shape formed by other 99 zebras, and then it can start chasing one of the other zebras, forcing it to go inside the shape, so the shape would not be convex anymore. Am I missing something? – JiK Feb 16 '15 at 14:02
  • I mean 100m apart. Thanks. Let me think a little. :) – Rok Kralj Feb 16 '15 at 14:03
  • Keep in mind the zebra ALSO has to be 100m away from the lion :) – Duncan Feb 16 '15 at 15:03
  • As JiK said, the zebras will need to stay more than 200m apart in order for there not to exist a point P that is within 100m of each of them. Also, you don't prove that it's not possible for the lion to force a zebra to jump within 200m of another zebra. Just being a convex shape won't do it, as the lion should be able to eventually get outside (as only one zebra can move at a time) and start chasing the zebras in toward each other. – glibdud Feb 19 '15 at 20:08
-13

Answer

Quick answer: The zebras would survive forever.

Simple explanation:

The key concept here is "infinite plane". Since the plane is infinite, positioning is irrelevant, except for the fact that the zebras are placed at great distances from each other and the lion. The closest zebra from the lion simply moves away from the lion in a direction that does not bring it near the path of another zebra. Because the plane is infinite, the zebras can be a nearly infinite distance from each other, thus making their escape paths very easy to avoid other zebras.

Michael Rize
  • 2,405
  • 1
  • 19
  • 39
  • 4
    The lion could go round a nearby deer (100-200m) such that 2 deer lie on the same line. Then he could chase the near one, and eventually encounter the far one. The angle of choice of direction for a particular deer is determined by its distance from the lion, so a more elaborate proof will be required. – ghosts_in_the_code Feb 16 '15 at 12:57
  • Game rules state " the 100 zebras may arbitrarily pick their 100 starting positions" which, on an infinite plane could be trillions of light years from each other. How can you circle the zebra if you only can go 100 meters per move? – Michael Rize Feb 16 '15 at 13:03
  • If you come within 1 metre of a particular zebra from the left, it has no choice but to go right. Of course, you can't get so close immediately, but you can take advantage of the fact that by increasing the distance of 1 deer from you, the player is compromising the distance of 99 other deer. – ghosts_in_the_code Feb 16 '15 at 13:05
  • I believe in what you are saying, but your proof is not enough. – ghosts_in_the_code Feb 16 '15 at 13:06
  • I added to my answer – Michael Rize Feb 16 '15 at 13:18
  • No! The Archimedean_property disproves your assumption. – dmg Feb 16 '15 at 13:18
  • I did not say they are infinitely far away, I said close to infinitely far.. big difference :-P – Michael Rize Feb 16 '15 at 13:20
  • Yes, and that difference implies that you are not correct. Just dropping "trillions of light years away" and using it as it is infinity won't cut it. – dmg Feb 16 '15 at 13:21
  • "the steppe (= an infinite plane)" says in the description. – Michael Rize Feb 16 '15 at 13:22
  • 3
    "trillions of light years away" <> infinity :) – dmg Feb 16 '15 at 13:23
  • I don't see the reasoning behind the answer. The lion can start chasing zebra 1 until it is on a line with zebras 2 and 3. Then it can start chasing zebra 2 until zebra 2 reaches zebra 3, after which it will start chasing both of them, getting closer every step. Your answer does not give a strategy for the zebras to avoid that. – JiK Feb 16 '15 at 13:23
  • @JiK I was thinking about something like that, but zebra 2 can make a slight turn to the left/right, thus breaking the aligning of zebra 2, zebra 3 and the lion. – dmg Feb 16 '15 at 13:26
  • 1
    @dmg It can, but who knows what strategy the lion then might have, possibly involving the 97 other zebras? My point was not that the lion can catch the zebras, I just said that this answer is very incomplete. – JiK Feb 16 '15 at 13:28
  • @JiK I agree with you about that as you can see by my other comments. – dmg Feb 16 '15 at 13:29
  • you guys like to make me work. ok added more explanation to to the answer. – Michael Rize Feb 16 '15 at 13:30
  • the zebra is part of the circle.. that one zebra is making that part of the circle bigger, thus making the whole circle bigger – Michael Rize Feb 16 '15 at 13:31
  • Rephrasing my comment: "To refute those who think that it is possible for the lion get on the same line as two zebras:" I don't see how that refutes anything. The lion chases zebra 1, and only zebra 1 moves. The other zebras don't move. The lion will eventually get to line with zebras 2 and 3, because only zebra 1 moves, not zebras 2 and 3. I don't see how "circling all zebras" is related to getting on a line with two zebras. – JiK Feb 16 '15 at 13:34
  • 4
    For all intents and purposes, 10km (100km) is the same as "trillions of light years" in this case. – No. 7892142 Feb 16 '15 at 13:34
  • 1
    The radius of the lion's "circle" (not a real circle, imagine it to be easier to understand) increases with 100m per move. The radius of the zebras' circle increases with an average of 2m per move (200 meters for 100 moves). It is quite obvious that the lion will penetrate the circle of zebras :) – dmg Feb 16 '15 at 13:44
  • The circle does not need to expand in every direction, only the direction that the lion is heading in. If the lion chooses a new target zebra, then that direction is expanding as well. The lion will never penetrate the circle. – Michael Rize Feb 16 '15 at 13:57
  • @MichaelRize What do you mean by "the circle"? – JiK Feb 16 '15 at 13:58
  • Zebras are encircling the lion at a great distance from the lion and also from each other. – Michael Rize Feb 16 '15 at 14:00
  • The strategy is that the closest zebra will simply move 100 meters further away in the one direction that brings the zebra further not only from the lion, but from the neighboring zebras as well. The zebra's movement will never go closer to another zebra. – Michael Rize Feb 16 '15 at 14:04
  • "in the one direction that brings the zebra further not only from the lion, but from the neighboring zebras as well" I don't see why such a direction would always exist. And if the zebra moves to other direction than directly opposite to the lion, the lion will be closer to it after the next step, (although it probably won't be able to make the distance decrease without limit with a naive strategy). – JiK Feb 16 '15 at 14:07
  • @MichaelRize But if only one zebra moves then the lion will be able to get two aligned zebras at some moment. – dmg Feb 16 '15 at 14:12
  • 2
    Your strategy sucks. By long approach the lion can get two zebras lined up while having always been closer to a different zebra than the ones being lined up. Once lined up, charge. – Joshua Feb 16 '15 at 16:39
  • Joshua, dmg and JiK, if you have a better solution, post it. It is easy to criticize, but now try doing something constructive. – Michael Rize Feb 16 '15 at 17:02
  • 14
    @MichaelRize We are trying to do something constructive - trying to help you see why we think this is not a complete and convincing answer to the question. – JiK Feb 16 '15 at 17:37
  • @jik Seems to me that if it isn't a complete and convincing answer, there will be a scenario which refutes it. Providing such a scenario might be the best way to achieve your goal. – BobRodes Feb 17 '15 at 20:11
  • 1
    @BobRodes We are having trouble understanding the exact strategy the zebras use in this answer, so going as far as providing a counterexample feels quite impossible. – JiK Feb 17 '15 at 21:26
  • The strategy is to move the zebra closest to the lion directly away from the lion. The starting position is a large circle around the lion. If this is the strategy and starting position, then a zebra can be caught. – Trenin Feb 19 '15 at 15:07
  • (cont) The lion will moved towards a zebra. That zebra will move away. Keep going until the lion reaches the point that the zebra occupied on the original circle. At this point, you have 99 zebras and a lion in a circle and one zebra far away. Draw a line between the lion and the zebra he is chasing, and draw another line between the two zebras directly to his right. The lion should then aim for the intersection of these lines. When he gets there, the zebra he was chasing is no closer, but the two on the right are in a line with him. Now all he needs to do is chase them down. – Trenin Feb 19 '15 at 15:10
  • (cont) The closer zebra will eventually catch up to the far one, and then when they move away from the lion, they will be moving half as fast. The lion will eventually catch the both of them. – Trenin Feb 19 '15 at 15:11
  • @Trenin Note that if the lion chases a single zebra, that zebra will not be the only zebra to flee, as pretty quickly the zebra's neighbors will actually become the closest to the lion. Therefore, when the lion reaches the original circle, it won't be a single circle with one zebra outside, it'll look more like a circle with a smaller semicircle (roughly centered on the lion) stuck to it. But I agree with the spirit of your counterexample. At that point, the lion will be in a position to approach multiple zebras simultaneously, and this solution doesn't address what the zebras should do then. – glibdud Feb 19 '15 at 16:17
  • @glibdud Good point. – Trenin Feb 19 '15 at 16:31
  • 1
    The important point is that the lion will eventually make it outside the circle occupied by the zebras, and most of them will not have moved. If he then turns 90 degrees and runs in a slightly larger concentric circle, the end result will be that the zebras' circle will have shrunken a bit. If he continues to run in a slowly shrinking spiral, he should be able to eventually concentrate most of the zebras into a small area, at which he can charge, as they won't be able to all escape in time. – glibdud Feb 19 '15 at 19:57
  • @Trenin and glibdud , I believe you both are forgetting the distances involved. And your same argument can be applied to the popular answer above, with more effect and efficiency, since it is much easier to get multiple zebras on one line (and they are much closer together). However in my answer, there are 25 zebras per quadrant, each zebra is so far out, that approaching one zebra, will bring the lion further from the majority of other zebras. To me, my answer is glaringly obvious and I am puzzled why people are choosing a weaker answer. – Michael Rize Feb 19 '15 at 22:46
  • 2
    @MichaelRize Lopsy's solution is popular because it is complete and provable. Lining the zebras up in that solution is useless because of the constraints put on their movement. Yours has no such constraint. You seem to be just relying on the fact that it's a really long distance, but that's irrelevant given the unlimited time scale. I gave you a perfectly reasonable scenario for the lion to beat your strategy. Feel free to directly refute it. – glibdud Feb 20 '15 at 02:55
  • I directly refute it because my zebras are further away from each other than the other solution, and because they are not lined up in a straight line like the popular solution, they are less easy for the lion to line up and intercept. – Michael Rize Feb 20 '15 at 03:21
  • in fact, the other two solutions are contained within my solution, because the zebras are more than 200 or 300 meters apart, the zebras can evade the lion in the exact same way. The only difference is that I made the distances even greater to prove the ridiculousness of this puzzle. My solution is also the only one to take advantage of the "infinite plane". – Michael Rize Feb 20 '15 at 03:25
  • for example, each zebra can be compared to a star in the sky. But in this case the stars are on a flat plane. The lion can move toward one star (star representing a zebra) , but meanwhile that star is moving away from the lion at the same rate of speed. If the lion changes direction to another star, the same thing happens. Never will he get close enough to a zebra or zebras to catch one. – Michael Rize Feb 20 '15 at 03:27
  • Also, my solution does have a constraint. The zebras move away from the lion, in a direction that also moves it further from the other zebras. This direction is always possible, if you have a pencil and paper it is easily provable. I just didn't feel like making a diagram. – Michael Rize Feb 20 '15 at 03:32
  • 2
    @MichaelRize You don't seem to understand that while one zebra is fleeing the lion, the rest are remaining still. And since your zebras are not constrained to separate spaces like Lopsy's, the lion can chase one zebra until two others are lined up, then chase the closer of those two until he reaches the second, then he'll be able to gain on those two as they are forced to take turns moving. You have to prove that there's no way for the lion to herd the zebras, and you've not made any attempt to do so. You only cite the "great distance", which is irrelevant in an unlimited time scale. – glibdud Feb 20 '15 at 03:33
  • My zebras are definitely constrained to separate spaces with a fixed path. See the diagram. – Michael Rize Feb 20 '15 at 03:56
  • @MichaelRize Ok, good, that clarifies your strategy. But since only one zebra can move at a time, the lion can get outside the circle. And once he does, if he runs around the outside, the zebras will have to flee inward, toward the center of the circle, bringing them closer together. The lion can herd them as per my example above. – glibdud Feb 20 '15 at 04:00
  • I just posted an image proving that the other solution is worse, since the zebras are already lined up for the lion. – Michael Rize Feb 20 '15 at 04:05
  • @glibdud the lion moves up to 100m (if he is moving in a straight line) a circle is not a straight line, so if he was trying to circle, he would actually be covering less distance than the zebras. Also see my diagram proving the other solution is worse. – Michael Rize Feb 20 '15 at 04:24
  • 2
    @MichaelRize Ok, let's start again. You've shown us the initial configuration of your zebras and the lines they need to stay on. Now tell us exactly how they determine on their turns which zebra moves and in which direction. – glibdud Feb 20 '15 at 11:57
  • 2
    And if you want to disprove Lopsy's strategy, give us a real example with real numbers showing exactly how a lion captures a zebra. Your drawing shows nothing. – glibdud Feb 20 '15 at 11:59
  • Attempting to move the discussion to chat, though it's missing some recent comments. I'll make a few assumptions about the zebras' strategy and provide a lion's strategy, and you can go from there. – glibdud Feb 20 '15 at 14:43
  • @glibdud The drawing illustrates exactly your point about getting multiple zebras on the same line is more likely with the first answer. – Michael Rize Feb 20 '15 at 14:43
  • @MichaelRize As I said, getting zebras in line is irrelevant in Lopsy's solution because of how the zebras are constrained. You'll have to go farther and show exactly how the lion catches a zebra. In the meantime, go to the chat link in my last comment and give us the parameters on how the zebras in your strategy determine who moves and where. Then I'll provide an opposing lion strategy. – glibdud Feb 20 '15 at 14:48
  • (And yes, with your clarified constraints, lining up the zebras is now irrelevant against your strategy as well. There are other issues though, which I will illustrate once you've completed the description.) – glibdud Feb 20 '15 at 14:52
  • @MichaelRize See my answer which is a counter to yours. – Trenin Feb 20 '15 at 15:15
  • @glibdud Provided an answer which counters this answer. Hopefully that is sufficient to see why this won't work. – Trenin Feb 20 '15 at 15:15
  • @Trenin Feel free to add to the chat. Near as I can tell, the cognitive wall we're hitting here is the difference between "infinite" and "arbitrarily large". – glibdud Feb 20 '15 at 15:55
  • I greatly simplified my answer, because I concluded that zebra positioning is irrelevant on an infinite plane, only distance is. – Michael Rize Feb 21 '15 at 05:48
  • @glibdud After further reasoning I concluded that positioning is completely irrelevant on an infinite plan, only distance is. So I revised my answer to reflect that. – Michael Rize Feb 21 '15 at 05:52
  • 2
    @MichaelRize You still don't seem to understand that with an unlimited timeline, distance is irrelevant. The space between zebras is still finite, so regardless of their positioning, a finite-size circle could still be drawn around them, and the lion could get outside that circle and could conceivably chase them toward the center, ever closer to each other. Your answer now just amounts to "trust me, the lion can't catch them". No attempt at providing an actual strategy for the zebras, or a proof that they don't need one. – glibdud Feb 21 '15 at 15:19
  • @glibdud, you still don't seem to understand what infinite space is. If you did, you would understand that the only thing that matters is distance. The zebras have all the room they need to evade the lion. There are no physical constraints so talking about positioning is useless. All positions will work if there are 10,000 miles between each zebra. The zebra only needs to be not going into a direction that will lead to another zebra, and always provide a minimum space between zebras. Simple and done. – Michael Rize Feb 21 '15 at 16:01
  • @MichaelRize You haven't proven that there will always exist a direction that leads away from the lion and all other zebras. – glibdud Feb 21 '15 at 16:15
  • 5
    You're describing what a strategy should do, but you're not actually providing one. – glibdud Feb 21 '15 at 16:19
  • 2
    @MichaelRize I agree with glibdud. You say that they can stay away by basically, "staying away from the lion" without proving how they do so. If they only move on lines extending from the origin, then my answer shows a counter example. If they move in different directions, then you are probably right, but still need to prove it. Handwaving and saying trillions of light years isn't enough. – Trenin Feb 23 '15 at 13:36
  • By your argument, I could say that a lion moving twice as fast as a zebra would never catch the zebra because the zebra is "nearly infinite distance away" from the lion initially. And nearly infinite may as well be infinite right? So that means the lion can never catch up. – Trenin Feb 23 '15 at 13:39
  • @Trenin What people don't seem to understand, is that with infinite space, the lion will only ever be facing one zebra at a time. So the lion is not moving twice as fast as the zebra it is chasing; they are going the same speed. The only way the lion can "see" two or more zebras at once, is if the zebra stupidly leads the lion to another zebra, but the zebra would never do that, and the lion cannot force a zebra to do that because of the nearly infinite spacing between zebras. – Michael Rize Feb 24 '15 at 03:53
  • Infinite spacing makes positioning so irrelevant that, even if the lion has all 100 zebras lined up in a straight line, each zebra only has to go diagonally to the left or the right. – Michael Rize Feb 24 '15 at 03:56