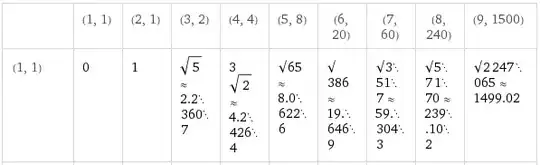
Can you work out how this number sequence is built up? Can you work out how it continues?
1, 1, 2, 4, 8, 20, 60, 240, 1500, .......
Hint 1
this is a mathematical puzzle
Hint 2
It does not involve complicated mathematics
From time to time hints will be updated.
Note: this sequence cannot be found in The On-Line Encyclopedia of Integer Sequences