Ripple effects: A suite of puzzles and conundrums

Question

Best explained here.

Basically there are two rules:

• fill in each region with the numbers 1 to N, where N is the size of that region
• two numbers, both K, cannot both be in the same row or column if they are less than or equal to K squares away. e.g the red squares cannot be 3.

Puzzles

I was wrapped up in making ripple effects back in the day so here are some:

Yellow squares are a number from 1-5.

Also, the puzzles are disjoint (e.g each grid is its own puzzle), so I guess you can post partials if you solve, say, 1 puzzle I guess.

There was going to be a meta-puzzle but I decided to scrap it. You might see some artefacts of the meta around.

Conundrums

1. Show that for n>1, n 1xn pieces in a row is bad. n=4 shown below

2. Show that on an infinite grid, if all regions are the same size then the ripple effect fails.
3. What is the smallest number n such that there exists a ripple effect puzzle, which can be extended to infinity, such that all regions are size at most n?
4. Two 1x2 pieces can be positioned to make a uniquely solvable ripple effect (shown below). How many 1x3 pieces do you need?

5. (cont.) What about 1x4 pieces? Note: I have not solved this yet

Bonus: Generalise (all of) the above to k dimensions

I did make a bunch more small puzzles and conundrums (~5-10 or so) but my organisation is awful so they kind of... disappeared. Sorry about that. I might post them if they turn up.

Answer 1

Partial answer - $\color{red}{\text{Warning - solutions are not spoilered}}$

Order of solve, decomposed into 3 levels:

^{Sorry to the colourblind}

1. Red, orange, light green, dark green, light blue, dark blue, purple, brown
2. Thick lines, thin lines
3. No dot, 1 dot

Solutions to all puzzles

Puzzle 1

NB: the ? should be a 0 to make the word ENCRYPT using AZ26

Puzzle 2

Puzzle 3

Puzzle 4

Puzzle 5

Puzzle 6

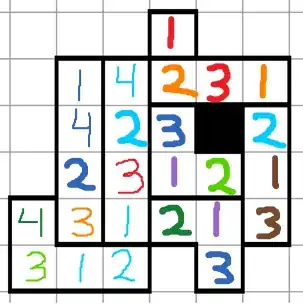
Puzzle 7

NB: For puzzles 3, 4 and especially 5, there was quite a bit of casework, which has been omitted from the presented solution, but please feel free to ask me if you need help following a particular step (having done all previous steps).

Solutions to conundrum 1 and 3 and informal solution to 2

Conundrum 1

Label the boxes $1, 2, 3, \dots, n$ and the cells within box $i$ $(i,1), (i,2), (i,3), \dots, (i,n)$.

Observe that if the number $n$ is in $(i,j)$, the number $n$ can't be in $(i,j+1),(i,j+2),\dots,(i,n)$ or $(i+1,1),(i+1,2),\dots,(i+1,j)$ .

So no matter where the number $n$ is in box $1$, it cannot be in $(2,1)$. And no matter where the number $n$ is in box $2$ apart from $(2,1)$, it can't be in either $(3,1)$ or $(3,2)$.

We can extend this argument by induction to say that if the number $n$ is in cell $(i,j)$, $i\leq j$. By symmetry, $i\geq j$.

Therefore the number $n$ can only be in cells which have the form $(x,x)$, for some $1\leq x\leq n$.

Now, consider the number $n-1$. If it is in cell $(i,j)$, it can't be in $(i,j+1),(i,j+2),\dots,(i,n)$ or $(i+1,1),(i+1,2),\dots,(i+1,j-1)$ .

So no matter where $n-1$ is in box 1, since it can't be in $(1,1)$, it can't be in $(2,1)$ either. And no matter where $n-1$ is in box 2, since it can't be in $(2,1)$ or $(2,2)$, it can't be in $(3,1)$, $(3,2)$ or $(3,3)$.

We can extend this argument by induction to say that if the number $n$ is in cell $(i,j)$, $i<j$. By symmetry, $i>j$. But this is absurd, so a ripple effect puzzle with $n$ $1\times n$ pieces in a line is not solvable.

NB: 'By symmetry' applies because we can extend the argument identically, but from the other end of the line.

Conundrum 2 (informal solution)

Suppose the regions are all of size $n$.

The density of the number $n$ in an arbitrary region should be $\frac{1}{n}$, since each region has $1$ $n$ out of $n$ squares.

However, each $n$ eliminates $4n$ squares (with multiplicity) from being $n$, and each square can be eliminated up to $4$ times, so there should be about $n$ non-$n$ squares for every $n$ squares, leading to a density of $\frac{1}{n+1}$.

But $\frac{1}{n}\neq\frac{1}{n+1}$, contradiction.

Obviously, the notion of 'density' needs work on, but this is an intuitive outline to a potential solution.

Conundrum 3

Solve path:

• Black - lone 1s
• Red - 1s can't be anywhere else in the box
• Blue - Forced infinite ripple - either nothing but 3 can go in the cell, or nothing but 2 can go in the cell
• Green - Last cell in the box
• Orange - 2s and 3s can't be anywhere else in the box

Minimality:

Suppose we had only regions of size 1 - then we would have only 1s and two 1s would be adjacent.

Suppose we had only regions of size 1 or 2 - then we would have only 1s and 2s. Then either we have all 1s, all 2s, both are which are bad as above, or a 1 and 2 next to each other. But then neither 1 nor 2 can be in the cell on the opposite side of the 1 to the 2.

So 3 is the smallest n that works.