First, draw out a 10x10 grid. Take the shape below and see how many you can fit in the 10x10 grid. It should take up 6 grid squares. Also, it can be rotated.
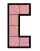
1) How many can you fit in the grid?
2) Can you prove that this is the most possible?
All credit goes to "Math Nite" at the University of Calgary
