5

This cube has a positive (blue) and a negative (black) bar on each face. That is 2 flat bars per face. On each face 1 bar has the opposite polarity to the other. I have hidden the faces to make the problem clearer.

I only want to run a single wire for positive and a single wire for negative. The wires will come in through the open ended bars, but I only want to run 2 wires. The open ended bars will not join.

Is there a way to route this so that every blue touches another blue, and every black touches another black? Right now 1 black bar (lower right) is isolated.

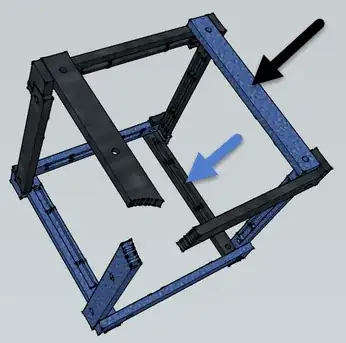
enter image description here

CarbonMan
  • 153
  • 3
  • 1
    This question could do with some clarification. Is the bite taken out of the near corner an actual part of the puzzle? Is that what you mean by "open ended bars" or is that referring to something else? If it is what you mean, does "will not join" mean "need not be connected" or "don't connect at the broken corner, hence need connecting elsewhere"? – Gareth McCaughan Jul 25 '17 at 09:30
  • @GarethMcCaughan the bite taken out is where the wires come in. Yes they are the open ended bars. The bars will not be connected in that corner. – CarbonMan Jul 25 '17 at 21:48

3 Answers3

6

I don't think it is possible.

Let's ignore the cut off corner, by imagining it is a completed cube. Suppose also that some valid choice of colours has been made such that each colour is all connected. Consider the 6 black bars. They cannot form a loop, as there is essentially only one way to do this and then the bars of the other colour would be disconnected. The same argument means that there is no blue loop either. In other words, each colour forms a tree graph.

Now cut off a cube corner as required. Whichever corner you choose to cut off, you will disconnect (at least) two bars of the same colour. The bars of that colour must then fall apart into two disconnected parts (otherwise it would have been a loop).

Jaap Scherphuis
  • 53,019
  • 7
  • 120
  • 208
2

This is

Not possible.

Because

Altogether you have 6 bars of each color, meaning you require at least 10 connections of blue-blue and black-black (5 each). Each corner does 2 connections if you have all 3 of the same color, 1 connection if you have 2 of one and 1 of other color, and the chewed off part has 0 connections. So, at minimum, you require 3 corners with all 3 of the same color (4 with 1/2, and the chewed off corner is arbitrary).

.

Now, can we make 3 corners with all 3 rods the same color? Let's say the bottom right corner (the one with 3x blue on the image), has all colors the same. It is obviously impossible that either of the 3 corners next to it has 3 of the same color, as it would lead to having face with 2x same color connectors. So, 3 corners with all the same color connections need to be for example 3 of (0, 0, 0), (1, 1, 0), (0, 1, 1) and (1, 0, 1). Or 3 of the other 4 corners. Sounds great, we can have the thingy connected.

However,

There is a tiny little issue that makes everything impossible. If we have say 000 corner all blue, then 110, 011 and 101 can only be all black to not have the same color on the face. 2 faces even. But if then 110 is all black, 011 or 101 cannot be. So, we can have just 2 corners all of the same color, but we require 3 to satisfy the connectivity.

Zizy Archer
  • 2,150
  • 7
  • 15
1

Can't you switch these 2 bars? Will that not work? This way all black and all blue will be connected.

enter image description here

EDIT: This does not satisfy the "at least 1 of each bar per face" requirement.

Forklift
  • 2,011
  • 10
  • 26
  • "On each face 1 bar has the opposite polarity to the other" i.e. each face has two flat sides of the bars, and one must be blue and one must be black. After your swap the top face has two black bars. – Jaap Scherphuis Jul 25 '17 at 12:42
  • @JaapScherphuis, right yes. Then I think this text from your answer is most appropriate: Whichever corner you choose to cut off, you will disconnect (at least) two bars of the same colour. – Forklift Jul 25 '17 at 12:43
  • @JaapScherphuis; the current cube has this already, e.g. back right face – JMP Jul 25 '17 at 13:12
  • @JaapScherphuis; which i think is ok, but Forklift gives a solid blue base – JMP Jul 25 '17 at 13:14
  • @JonMarkPerry: The OP's cube does not have that. Each face has only 2 parallel bars, of which one is blue, the other is black. Remember that the bars are like planks of wood, and only their wide (or "flat" in the OP) sides count. – Jaap Scherphuis Jul 25 '17 at 13:18