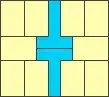
Let's pack some (one or more) T hexominoes together with some (one or more) small $a\times b$ rectangles into some bigger $m\times n$ rectangle without holes and overlapping pieces.
For example, I can pack two T hexominoes and eight $1\times1$ rectangles into a $5\times4$ rectangle:

Task
Find as many as you can different integer pairs $\{a,b\}$ so that one or more rectangles of size $a\times b$ can be packed together with T hexominoes into a $m\times n$ rectangle without holes and overlapping pieces.
Provide images of solutions if you claim that some combination is possible. Please, put your images in spoiler tags so that other users can try find themselves.
If some answers will have same number of pairs $\{a,b\}$, then answer with smaller total area of outer rectangles on example images is preferable. If area also equal, then earlier posted answer is preferable.
EDIT: Please, add to your answers total area of outer rectangles. If one tiling implicitly includes several $a\times b$ rectangles, then multiply area by number of combinations it includes.
Notes
I can guarantee that there exist solutions following integer pairs:
$1\times1$, $1\times2$, $1\times3$, $1\times4$, $1\times5$, $1\times6$, $1\times8$, $1\times9$,
$2\times2$, $2\times3$, $2\times4$, $2\times5$, $2\times6$
I'm wondering why a $1\times7$ rectangle solution is hard to find (maybe it's impossible?) when there exist solutions for with $1\times8$ and $1\times9$ rectangles.
1 week after posting, I'll put up my own answers for unfound combinations.